6. přednáška

$$\xdef\scal#1#2{\langle #1, #2 \rangle} \xdef\norm#1{\left\lVert #1 \right\rVert} \xdef\dist{\rho} \xdef\and{\&}\xdef\AND{\quad \and \quad}\xdef\brackets#1{\left\{ #1 \right\}} \xdef\parc#1#2{\frac {\partial #1}{\partial #2}} \xdef\mtr#1{\begin{pmatrix}#1\end{pmatrix}} \xdef\bm#1{\boldsymbol{#1}} \xdef\mcal#1{\mathcal{#1}} \xdef\vv#1{\mathbf{#1}}\xdef\vvp#1{\pmb{#1}} \xdef\ve{\varepsilon} \xdef\l{\lambda} \xdef\th{\vartheta} \xdef\a{\alpha} \xdef\vf{\varphi} \xdef\Tagged#1{(\text{#1})} \xdef\tagged*#1{\text{#1}} \xdef\tagEqHere#1#2{\href{#2\#eq-#1}{(\text{#1})}} \xdef\tagDeHere#1#2{\href{#2\#de-#1}{\text{#1}}} \xdef\tagEq#1{\href{\#eq-#1}{(\text{#1})}} \xdef\tagDe#1{\href{\#de-#1}{\text{#1}}} \xdef\T#1{\htmlId{eq-#1}{#1}} \xdef\D#1{\htmlId{de-#1}{\vv{#1}}} \xdef\conv#1{\mathrm{conv}\, #1} \xdef\cone#1{\mathrm{cone}\, #1} \xdef\aff#1{\mathrm{aff}\, #1} \xdef\lin#1{\mathrm{Lin}\, #1} \xdef\span#1{\mathrm{span}\, #1} \xdef\O{\mathcal O} \xdef\ri#1{\mathrm{ri}\, #1} \xdef\rd#1{\mathrm{r}\partial\, #1} \xdef\interior#1{\mathrm{int}\, #1} \xdef\proj{\Pi} \xdef\epi#1{\mathrm{epi}\, #1} \xdef\grad#1{\mathrm{grad}\, #1} \xdef\gradT#1{\mathrm{grad}^T #1} \xdef\gradx#1{\mathrm{grad}_x #1} \xdef\hess#1{\nabla^2\, #1} \xdef\hessx#1{\nabla^2_x #1} \xdef\jacobx#1{D_x #1} \xdef\jacob#1{D #1} \xdef\subdif#1{\partial #1} \xdef\co#1{\mathrm{co}\, #1} \xdef\iter#1{^{[#1]}} \xdef\str{^*} \xdef\spv{\mcal V} \xdef\civ{\mcal U} \xdef\other#1{\hat{#1}} \xdef\xx{\vv x} \xdef\yy{\vv y}$$

Pokračování

Počítali jsme stacionární vektor $\vv x$ pro přechodovou matici $A$, tj. $$A \vv x = \vv x$$

Mějme počáteční pravděpodobnostní vektor $\vv x_0$ $$\vv x_0 = \mtr{ p_0 q_0 \\ p_0(1 - q_0) \\ (1 - p_0) q_0 \\ (1 - p_0)(1 - q_0) }$$ A jistě $$\vv x_1 = A \vv x_0, \\ \xx_2 = A \xx_1 = A^2 \xx_0$$ Navíc $$w(\xx_0 + \delta A\xx_0 + \delta^2 A^2 \xx_0 + \dots) = \\ w(E + \delta A + \delta^2 A^2 + \dots) \xx_0 = \\ w \underbrace{(\overbrace{E - \delta A}^B)^{-1} \xx_0}_{\yy},$$ což je tedy $$\yy = B^{-1} \xx_0 \\ B \yy = \xx_0 \\ \yy = \frac{|\cdot|}{|\cdot|}$$

A tím pádem dostaneme opět lineární závislost výhry na parametru $p_i$.

Evoluční algoritmy

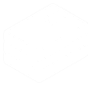
A počítejme $$\frac 1 3 1 + \frac 2 3 2 = \frac 5 3$$ $$\frac 1 3 0 + \frac 2 3 1,5 = 1$$

Úloha o dohodě

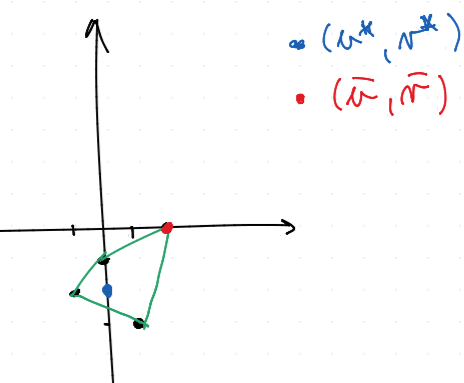
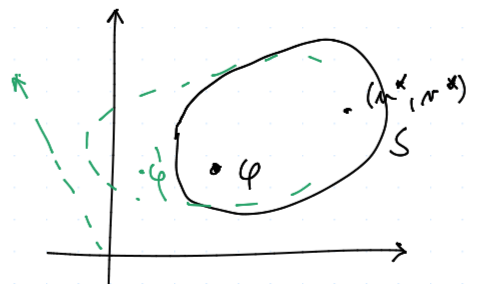
Nechť $\mcal D$ je množina všech úloh o dohodě (pouze hry 2 hračů) s funkci $\vf : \mcal D \to \R^2$.

Dále nechť úloha $(S, u\str, v\str)$, kde $S$ je konvexní a kompaktní podmnožina v $\R^2$ a $(u\str, v\str) \in S$ je výchozí dvojice výher, která je dána tím, co si hráči zaručí - přičemž hledá optimální situaci

$S$ je podmnožina, na které se mohou hráči "hýbat"

Požadavky na $\vf$

1. $\vf(S, u\str, v\str) \geq (u\str, v\str)$ (bavíme se pouze o výhrách - tzn. cca Paretovská optimalita)
2. $\vf(S, u\str, v\str, u\str) \in S$
3. $(u,v) \in S \land (u,v) \geq \vf(S, u\str, v\str) \implies (u,v) = \vf(S, u\str, v\str)$
4. $\vf(S, u\str ,v\str) \in T \subseteq S \land (u\str, v\str) \in T \implies \vf(T, u\str, v\str) = \vf(S, u\str, v\str)$
5. Invariance vůči translaci a afinní transformaci s kladným koeficientem ($\vf$ nemění polohu vůči $S$)
6. $S$ je symetrická vůči ose $x = y$ a $u\str = v\str$ $\implies \vf(S, u\str, v\str)$ leží na $x = y$
7. $(u\str, v\str) \in T \subseteq S \implies \vf(T, u\str, v\str) \leq \vf(S, u\str, v\str)$

Lze ukázat, že taková funkce $\vf$ splňující 1.-7. neexistuje

Podmínka 7. je velmi silná a pokazí nám to

Věta $\D{NASH}$

Existuje právě jedno $\vf$ splňující 1.-6..

Lemma $\D{L1}$

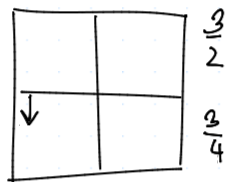
Nechť $(\exists u,v \in S) \quad u > u\str, v > v\str$, pak existuje jediné maximum funkce $g(u,v) = (u - u\str)(v - v\str)$ na množině $S_+ = \set{(u,v) \in S \mid u \geq u\str, v \geq v\str}$.

Důkaz

Jistě $g$ je spojitá, $S_+$ je kompaktní. Lze předpokládat, že $(u\str, v\str) = (0,0)$ (posunutím do počátku). Mějme $(u', v'), (u'', v'')$ maxima $g$.

Můžeme předpokládat, že $u' > u''$ a jistě i $v' < v''$. Potom $$g\left( \frac {u' + u''} 2, \frac {v' + v''} 2 \right) = \frac {(u' + u'')(v' + v'')} 4 = \\ \frac{u'v' + u''v' + u' v'' + u'' v''} 4 >^? g(u', v') = u'v' = u'' v''$$ Nerovnost odpovídá $$u'v'' + u'' v' > u'v' + u'' v'' \iff (u' - u'')(v'' - v') > 0,$$ což ale jistě platí. Tedy jsme našli nové maximum, což je spor. $\blacksquare$

Lemma $\D{L2}$

Za předpokladů $\tagDe{L1}$ nechť $$h(u,v) = (\bar v - v\str)u + (\bar u - u\str)v,$$ kde $(\bar u, \bar v)$ je bod, ve kterém se realizuje maximum $g$ z $\tagDe{L1}$. Pak pro libovolné $(u,v) \in S$ platí $h(u,v) \leq h(\bar u, \bar v)$.

Důkaz

Sporem, nechť $h(u,v) > h(\bar u, \bar v)$ pro nějaké $(u,v) \in S$. Nechť $\ve \in (0,1)$ a $$(u', v') = (\bar u, \bar v) + \ve ((u,v) - (\bar u, \bar v))$$ Pak ale $$h(u- \bar u, v - \bar v) = h(u,v) - h(\bar u, \bar v) > 0$$ Nyní dosaďme $$g(u', v') = (\bar u - \ve(u - \bar u) - u\str)(\bar v - \ve(v - \bar v) - v\str) = \\ = (\bar u - u\str)(\bar v - v\str) - \ve( (u -\bar u)(\bar v - v') + (\bar u - u\str)(v - \bar v)) + \ve^2(u - \bar u )(v - \bar v)$$ A derivací podle $\ve$ $$0 < \alpha + \beta \ve + \gamma \ve^2 \to \beta + 2 \gamma \ve,$$ tedy s růstem $\ve$ roste derivace na vhodném $(0, \ve_0)$. Tedy $g$ je rostoucí, což je spor s $\tagDe{L1}$.

Důkaz $\tagDe{NASH}$

Nastane právě jedna z možností

1. existuje $(u,v) \in S$ takové, že $u > u\str, v > v\str$
   
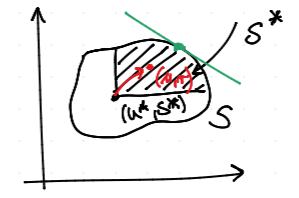
   Potom vezmeme $(\bar u, \bar v)$ z $\tagDe{L1}$.
2. Neplatí 1., ale existuje $(u,v) \in S$ takové, že $u > u\str$ (a $v = v\str$)
   
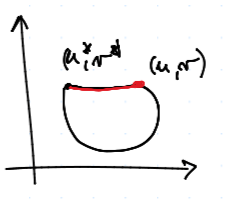
   V tomto případě vezmeme $\bar v = v\str$ a s $\bar u$ jdeme na maximum $(u \quad S)$
3. Neplatí 1., ale existuje $(u, v) \in S$ takové, že $v > v\str$ (a $u = u\str$)
   $\hspace{3cm}$ANALOGICKY
4. Neplatí nic, z 1. - 3., tzn. $\bar u = u\str$ a $\bar v = v\str$. $\blacksquare$

Příklad

Mějme bimaticovou hru

• student
  $$A = \begin{matrix}\text{učí} \\ \text{neučí}\end{matrix} \overbrace{\mtr{2 & - 1 \\ 1 & 0}}^{\text{dá} \;\; \text{nedá}}$$
• učitel
  $$B = \mtr{0 & - 2 \\ - 3 & -1}$$

U bimaticových her je $S$ konvexní obal všech situací a bodů z dolních hodnot

Zajímavější případ