Vektorový integrální počet
$$ \xdef\scal#1#2{\langle #1, #2 \rangle} \xdef\norm#1{\left\lVert #1 \right\rVert} \xdef\dist{\rho} \xdef\and{\&}\xdef\AND{\quad \and \quad}\xdef\set#1{\left\{ #1 \right\}}\xdef\brackets#1{\left( #1 \right)} \xdef\parc#1#2{\frac {\partial #1}{\partial #2}} \xdef\mtr#1{\begin{pmatrix}#1\end{pmatrix}} \xdef\bm#1{\boldsymbol{#1}} \xdef\mcal#1{\mathcal{#1}} \xdef\vv#1{\mathbf{#1}}\xdef\vvp#1{\pmb{#1}} \xdef\ve{\varepsilon} \xdef\l{\lambda} \xdef\th{\vartheta} \xdef\a{\alpha} \xdef\vf{\varphi} \xdef\Tagged#1{(\text{#1})} \xdef\tagged*#1{\text{#1}} \xdef\tagEqHere#1#2{\href{#2\#eq-#1}{(\text{#1})}} \xdef\tagDeHere#1#2{\href{#2\#de-#1}{\text{#1}}} \xdef\tagEq#1{\href{\#eq-#1}{(\text{#1})}} \xdef\tagDe#1{\href{\#de-#1}{\text{#1}}} \xdef\T#1{\htmlId{eq-#1}{#1}} \xdef\D#1{\htmlId{de-#1}{\vv{#1}}} \xdef\conv#1{\mathrm{conv}\, #1} \xdef\cone#1{\mathrm{cone}\, #1} \xdef\aff#1{\mathrm{aff}\, #1} \xdef\lin#1{\mathrm{Lin}\, #1} \xdef\span#1{\mathrm{span}\, #1} \xdef\O{\mathcal O} \xdef\ri#1{\mathrm{ri}\, #1} \xdef\rd#1{\mathrm{r}\partial\, #1} \xdef\interior#1{\mathrm{int}\, #1} \xdef\proj{\Pi} \xdef\epi#1{\mathrm{epi}\, #1} \xdef\grad#1{\mathrm{grad}\, #1} \xdef\gradT#1{\mathrm{grad}^T #1} \xdef\gradx#1{\mathrm{grad}_x #1} \xdef\hess#1{\nabla^2\, #1} \xdef\hessx#1{\nabla^2_x #1} \xdef\jacobx#1{D_x #1} \xdef\jacob#1{D #1} \xdef\subdif#1{\partial #1} \xdef\co#1{\mathrm{co}\, #1} \xdef\iter#1{^{[#1]}} \xdef\str{^*} \xdef\spv{\mcal V} \xdef\civ{\mcal U} \xdef\other#1{\hat{#1}} \xdef\xx{\vv x} \xdef\yy{\vv y} \xdef\partDiff#1{\frac{\partial}{\partial #1}} \xdef\partDeriv#1#2{\frac{\partial #1}{\partial #2}} \xdef\nPartDeriv#1#2#3{\frac{\partial^{#1} #2}{\partial #3}} \xdef\Div#1{\mathrm{div}\, #1}\xdef\rot#1{\mathrm{rot}\,#1} \xdef\d{\,\mathrm{d}} $$
Základní pojmy
Připomeňme definici jednoduchého oboru $\tilde V$ v $\R^3$ (Definice 23 v prezentacích), což je množina, která je sjednocením jednoduchých oborů vzhledem ke všem osám, přičemž jednoduchý obor $V$ vzhledem k např. ose $z$ definujeme jako
$$
V = \set{[x,y,z] \in \R^3 \mid [x,y,z] \in M, g(x)x,y) \leq yz \leq h(x)x,y)},
$$
kde $M \subseteq \R^3$ je množina v rovině, která je omezená uzavřenou jednoduchou křivkou $C$.
Jednoduchá křivka neprotíná sama sebe.
Definice $\D{ZD.1}$ (nabla operátor)
Hamiltonův nabla operátor definujeme v $\R^2$ jako $$ \nabla := \brackets{\partDiff x, \partDiff y}, $$ z čehož dostáváme, že funkci $f : \R^2 \to \R$ přiřazuje vektorové pole $$ \nabla f = \grad f = \brackets{ \partDeriv f x, \partDeriv f y}. $$ Obdobně bychom jej definovali pro $\R^n$.
Hamiltonův operátor $\nabla$ aplikovaný na vektorové pole $\vv F$ v bodě $[x,y]$ si můžeme představit jako změny $\vv F(x,y) \mapsto \vv F(\tilde x, \tilde y)$ při malém posunutí $[x,y] \mapsto [\tilde x, \tilde y]$. Potom skalární součin vektorového pole s tímto operátorem pak dává v jistém smyslu "průměr" jak je změna vektorového pole rovnoběžná se zmíněným malým posunem. Naopak vektorový součin těchto dvou členů dává "průměrnou" míru kolmosti změny vektorového pole a malé změny zkoumaného bodu.
Pro lepší intuici doporučuji toto video.
Uveďme jako poznámku, že operátor $\nabla \circ \nabla = \nabla^2 = \Delta$ se nazývá Laplaceův operátor a pro skalární funkci $f$ má tvar $$ \Delta f = \nPartDeriv{2}{f}{x^2} + \nPartDeriv{2}{f}{y^2} $$
Nabla operátor aplikovaný na vektorovou funkci $\vv F : \R^2 \to \R^2$ (tj. vektorové pole) dává Jakobiho matici $$\nabla \vv F = \mtr{\partDeriv {\vv F_1} x & \partDeriv {\vv F_1} y \ \partDeriv{\vv F_2} x & \partDeriv{\vv F_2} y}$$
Definice $\D{ZD.2}$ (divergence)
Nechť máme vektorovou funkci $\vv F(x,y) = (P(x,y), Q(x,y))$, kde funkce $P,Q: \R^2 \to \R$ jsou spojitě diferencovatelné.
Tedy jsou spojité spolu se svými prvními parciálními derivacemi
Pak s použitím definice $\tagDe{ZD.1}$ označíme divergenci vektorového pole jako funkci $\Div{} : \R^2 \to \R$ definovanou předpisem $$ \Div {\vv F} = \scal {\nabla} {\vv F} = \partDeriv P x + \partDeriv Q y = P_x + Q_y. $$ Obdobně bychom divergenci definovali pro vektorové pole v $\R^n$.
Dále si uvědomme, že divergence uvádá "poměr" přítoku a odtoku vektorového pole v daném bodě. To jest, je-li $\Div {\vv F}(x,y) > 0$, pak v bodě $[x,y]$ více vektorové odtéká, než je do toho bodu přítok. Analogicky pro situaci $\Div {\vv F}(x,y) < 0$.
V analogii s kapalinami by to byl bod, ze kterého kapalina více odtéká, než do něj přitéka - tj. v tomto bodě vzniká kapalina.
Má-li vektorové pole charakterizující nějakou kapalinu pozitivní divergenci, potom by se v něm skrvny (např. ropná skrvna v oceánu) zvětšovaly postupem času
Obdobně můžeme zapsat i totální diferenciál funkce $f:\R^n \to \R$ $$ \d f = \scal {\nabla f} {\d \vv x} = \partDeriv{f}{x_1} \d x_1 + \partDeriv{f}{x_2} \d x_2 + \dots + \partDeriv{f}{x_n} \d x_n $$
Definice $\D{ZD.3}$ (zřídlovost)
Vektorové pole $\vv F$ nazveme nezřídlové, pokud pro každý jeho bod $[x,y]$ platí $$ \Div {\vv F}(x,y) = 0. $$ V opačném případě jej nazveme zřídlové.
Definice $\D{ZD.4}$ (rotace, curl)
Nechť máme vektorovou funkci $\vv F(x,y,z) = (P(x,y,z), Q(x,y,z), R(x,y,z))$, kde funkce $P,Q,R: \R^3 \to \R$ jsou spojitě diferencovatelné.
Pak s použitím definice $\tagDe{ZD.1}$ označíme rotaci vektorové pole jako funkci $\rot{} :\R^3 \to \R^3$ s předpisem $$ \rot{\vv F} = \nabla \times \vv F = \brackets{R_y - Q_z, P_z - R_x, Q_x - P_y} $$
Pro dvourozměrné vektorové pole $\vv F : \R^2 \to \R^2$ pak uvažujeme rotaci jako $\rot{} : \R^3 \to \R^3$ s 3. vstupní souřadnicí vždy nulovou a platí $$ \rot{\vv F} = (0, 0, Q_x - P_y) $$
Zde je důležité si uvědomit, že ačkoliv pracujeme s 2D vektorovým polem, jeho rotace bude ležet ve 3. dimenzi, neboť musí být kolmá na jak na $\nabla$, tak i na vektorové pole $\vv F$.
Rotace $\rot{\vv F}(x,y)$ udává lokální míru rotace v bodě $[x,y]$ a je-li nulová, pak takové pole nazveme nevírové.
Je-li rotace $\rot{\vv F} > 0$ vektorového pole $\vv F$, pak se tato rotace děje proti směru hodinových ručiček z pohledu kladně orientovaného normálního vektoru (osy $z$ pro $\vv F: \R^2 \to \R^2$).
Lemma $\D{ZT.1}$ (vlastnosti rotace a divergence)
Nechť máme funkci $f: \R^n \to \R$ a vektorovou funkci $\vv F(\vv x) = (P_1(\vv x), \dots, P_n(\vv x))$, kde funkce $P_1, \dots, P_n: \R^n \to \R$ jsou spojitě diferencovatelné. Pak platí
- $\rot{\grad f} = \vv 0$
- $\Div{\rot{\vv F}} = 0$
Důkaz:
Důkaz provedeme pro každou část zvlášť. Pro první rovnost jistě platí
$$
\rot{\grad f} = \nabla \times \grad f = \nabla \times \nabla f,
$$
přičemž si zde můžeme uvědomit, že $\nabla f$ je de facto lineární násobek operátoru $\nabla$, tedy $\nabla$ a $\nabla f$ jsou lineárně závislé. Z tohoto plyne, že jejich vektorový součin je nulový vektor. Více rigorózně tento důkaz provedeme v $\R^3$ následovně
$$
\begin{aligned}
\rot{\grad f} &= \nabla \times \grad f = \nabla \times \brackets{\partDeriv{f}{x}, \partDeriv{f}{y}, \partDeriv{f}{z}} \
&= \brackets{ \nPartDeriv{2}{f}{zy} - \nPartDeriv{2}{f}{yz}, \nPartDeriv{2}{f}{zx} - \nPartDeriv{2}{f}{xz}, \nPartDeriv{2}{f}{yx} - \nPartDeriv{2}{f}{xy} } \
&= \vv 0,
\end{aligned}
$$
za předpokladu, že $f$ je dostatečně hladká. V $\R^n$ by se důkaz vedl obdobně.
Dokažme nyní druhou část tohoto lemmatu. Jistě
$$
\Div{\rot{\vv F}} = \scal {\nabla} {\rot \vv F} = \scal {\nabla} {\nabla \times \vv F},
$$
chápeme-li nyní $\nabla$ jako vektor, pak z definice vektorového součinu je $\nabla \times \vv F \perp \nabla \implies \scal {\nabla} {\nabla \times \vv F} = 0$. $\blacksquare$
Definice $\D{ZD.5}$ (křivkový integrál 2. druhu)
Uvažujme vektorové pole $\vv F : \R^2 \to \R^2$ a křivku $C$ charakterizovanou parametrizací $t \in [a,b], x = \vf(t), y = \psi(t)$. Potom integrál $$ \int_C \scal{\vv F} {\d \vv x} = \int_C \scal {\vv F} {\d \vec{l}} = \int_C \scal {\vv F} {\vec t} \d t, $$ kde $\d \vv x = \d \vec{l} = (\d x, \d y)$ a $\vec t = (\vf', \psi')$, nazveme křivkový integrál 2. druhu.
Křivkovým integrálem 2. druhu v jakémsi smyslu zobecňujeme koncept "práce" (z fyziky), přičemž standardně jsme zvyklí na vztah $W = F \cdot d$, kde $d$ je délka trajektorie a $F$ síla působící na těleso posunující ho po zmíněné trajektorii. Představit si můžeme například šikmou plochu, viz obrázek.
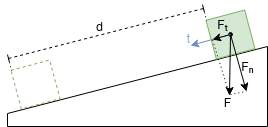
V této situaci gravitační pole působící silou $\vec F$ vykoná práci pouze části síly $F$, která je tečná (v tomto případě rovnoběžná) ke směru pohybu. Tato tečná část je označena $\vec F_t$ a jistě platí $\vec F_t = \scal{\vec{F}} {\vec {t}}$ a taktéž $$ W = |\vec F_t| \cdot d = \scal{\vec F} {\vec t} \cdot d $$ To ovšem můžeme zapsat i pomocí křivkového integrálu 2. druhu, který udává
- práci, kterou vykoná vektorové pole při posunu tělesa po trajektorii
Definice $\D{ZD.6}$ (plošný integrál 2. druhu)
Uvažujme vektorové pole $\vv F = (P(x,y,z),Q(x,y,z),R(x,y,z)) : \R^3 \to \R^3$ a plochu $S$. Potom $$ \iint_S \scal {\vv F} {\vec{n}} \d S = \iint_S P(x,y,z) \d y \d z + Q(x,y,z) \d x \d z + R(x,y,z) \d x \d y, $$ kde $\vec n$ je normálový vektor plochy $S$, nazýváme plošný integrál 2. druhu.
Plošný integrál 2. druhu nám udává průtok (flux) vektorového pole $\vv F$ skrze plochu $S$, který v každém bodě této plochy počítáme jako skalární součin normály $\vec{n}$ k ploše $S$ a vektorového pole $\vv F$ (což nám dá, jak "velká část" $\vv F$ směřuje ve směru normály $\vec{n}$ a tedy protíká onou plochou $S$)
Důležité vlastnosti
Věta $\D{VT.1}$ (Gaussova-Ostrogradského věta/Gauss divergence theorem)
Zformulujme tuto větu prvně slovně, poté i s podmínkami rigorózně:
Průtok vektorového pole $\vv F$ skrze ohraničenou plochu $S$ je roven integrálu z divergence $\Div{\vv F}$ přes celý objem $V$, který plocha $S$ ohraničuje.
Nechť $V$ je jednoduchý obor v $\R^3$, $\vv F : \R^3 \to \R^3$ je vektorové pole se spojitě diferencovatelnými složkami v každé proměnné a nechť $S$ je ohraničená plocha ohraničující $V$ orientovaná ve směru vnější normály. Pak platí $$ \iint_S \scal{\vv F} {\vec{n}} \d S = \iiint_V \Div{\vv F} \d V $$
Zde si uvědomme, že
- je-li kapalina nestačitelná (samovolně nemizí/nevzníká, tedy $\Div{\vv F} = 0$), potom stejná část "přiteče" do libovolné oblasti, jako z ní odteče
- stejně tak, točí-li se kapalina (vektorové pole $\vv F$) pouze v rámci této oblasti (tedy $\Div{\vv F}$ je opět nulový), pak jistě neproudí skrze plochu $S$
Abychom pochopili, proč můžeme průtok spočítat přes divergenci v celém objemu, rozdělme si objem $V$ uzavřený plochou $S$ na malé obdélníčky (kvádříky v $\R^3$) a spočítejme divergenci v těchto obdélnících (na obrázku jsou znázorněny všechny divergence kladné). Při dostatečně jemném dělení a spojitosti vektorového pole $\vv F$ zjistíme, že divergence mezi sousedícími stěnami se odečtou (znázorněno červeně) a zbudou nám pouze divergebce v "okrajovém pásu" (aka plocha $S$) mířící ven z $V$ (znázorněny modře).
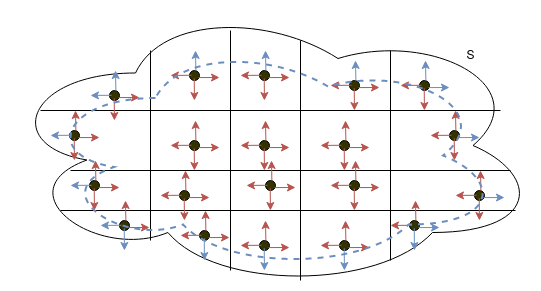
Poznamenejme, že znaménko průtoku dovnitř plochy $S$ je opačné, než znaménko průtoku vně této plochy. Aneb tuto větu můžeme interpretovat tak, že pokud dohromady (skrze integrál) uvnitř $V$ (respektive $S$) nevzniká ani nemizí žádná kapalina (vektorové pole $\vv F$), pak průtok skrze plochu $S$ musí být nulový (při znaménkové konvenci řečené výše).
Množina $G \subseteq \R^2$ je jednoduše souvislá oblast, pokud je $G$ otevřená, souvislá (libovolné 2 body lze spojit lomenou čarou, která leží v $G$) a s každou uzavřenou křivkou leží v $G$ i vnitřek této křivky.
Aneb každá uzavřená křivka v $G$ lze spojitě deformovat do bodu, aniž bychom $G$ opustili.
Věta $\D{VT.2}$ (Stokesova věta)
Nechť plochu $S$, která je omezená ohraničenou křivkou $C$ tvořící kraj $S$, lze rozložit na konečný počet částí, které jsou grafy funkcí proměnných $x,y$, totéž pro $x,z$ a $y,z$. Nechť vektorové pole $\vv F : S \to \R^3$ má spojitě diferencovatelné složky na $S$. Dále nechť křivka $C$ je orientovaná souhlasně s plochou $S$. Pak platí $$ \oint_C \scal{\vv F}{\d \vv x} = \iint_S \scal{\rot{\vv F}}{\vec n} \d S $$ nebo ekvivalentně $$ \oint_C \scal{\vv F}{\d \vec l} = \iint_S \scal{\rot{\vv F}}{\d \vec S} $$
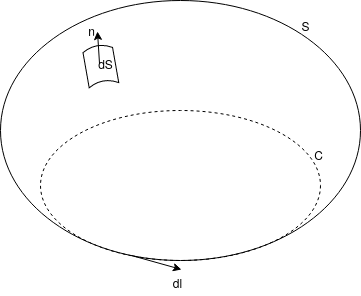
Geometrická odůvodnění si ukážeme na jednodušší variantě - na Greenově větě $\tagDe{VT.3}$.
Věta $\D{VT.3}$ (Greenova věta)
Greenova věta je speciální případ Stokesovy věty $\tagDe{VT.2}$ pro plochu $S$, zde značenou jako $G$, jakožto rovinu.
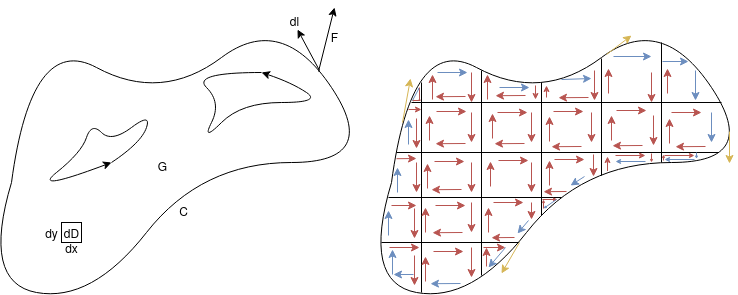
Nechť $G$ je jednoduše souvislá oblast v rovině, $C$ je uzavřená, kladně orientovaná (proti směru hod. ručiček) křivka v $G$. Dále nechť $\vv F : \R^2 \to \R^2$ je vektorové pole se spojitě diferencovatelnými složkami na uzávěru $\overline G$. Pak platí $$ \oint_C \scal{\vv F}{\d \vv x} = \iint_D \rot {\vv F} \overbrace{\d x \d y}^{\d D}, $$ kde $D$ je část množiny $G$ omezená křivkou $C$ a $\d \vec{l} = \d \vv x = (\d x, \d y)$ udává tečnu ke křivce $C$ v daném bodě.
Opět tuto větu odůvodníme podobným argumentem jako u Gaussovy věty $\tagDe{VT.1}$, tj. tentokrát plochu $S$ rozdělíme na obdélníčky, ve kterých určíme rotaci vektorového pole $\rot{\vv F}$. Zjemňujeme-li toto dělení, všimneme si, že sousedí-li 2 obdélníčky a mají stejně orientovanou rotaci, pak se na sdílené straně "potkají 2 protichůdné směry" a celkem se rotace "odečte". Tímto nám opět zbude pouze rotace na okraji oblasti $G$, tedy křivka $C$, při které je rotace tečná ke křivce $C$ - to je ale přesně integrál skalárního součinu vektorového pole $\vv F$ a malého tečného kroku na křivce $C$, tj. $d \vec{l}$.