Skip to main content

Vektorový integrální počet

\xdef\scal#1#2{\langle #1, #2 \rangle} \xdef\norm#1{\left\lVert #1 \right\rVert} \xdef\dist{\rho} \xdef\and{\&}\xdef\AND{\quad \and \quad}\xdef\set#1{\left\{ #1 \right\}}\xdef\brackets#1{\left( #1 \right)} \xdef\parc#1#2{\frac {\partial #1}{\partial #2}} \xdef\mtr#1{\begin{pmatrix}#1\end{pmatrix}} \xdef\bm#1{\boldsymbol{#1}} \xdef\mcal#1{\mathcal{#1}} \xdef\vv#1{\mathbf{#1}}\xdef\vvp#1{\pmb{#1}} \xdef\ve{\varepsilon} \xdef\l{\lambda} \xdef\th{\vartheta} \xdef\a{\alpha} \xdef\vf{\varphi} \xdef\Tagged#1{(\text{#1})} \xdef\tagged*#1{\text{#1}} \xdef\tagEqHere#1#2{\href{#2\#eq-#1}{(\text{#1})}} \xdef\tagDeHere#1#2{\href{#2\#de-#1}{\text{#1}}} \xdef\tagEq#1{\href{\#eq-#1}{(\text{#1})}} \xdef\tagDe#1{\href{\#de-#1}{\text{#1}}} \xdef\T#1{\htmlId{eq-#1}{#1}} \xdef\D#1{\htmlId{de-#1}{\vv{#1}}} \xdef\conv#1{\mathrm{conv}\, #1} \xdef\cone#1{\mathrm{cone}\, #1} \xdef\aff#1{\mathrm{aff}\, #1} \xdef\lin#1{\mathrm{Lin}\, #1} \xdef\span#1{\mathrm{span}\, #1} \xdef\O{\mathcal O} \xdef\ri#1{\mathrm{ri}\, #1} \xdef\rd#1{\mathrm{r}\partial\, #1} \xdef\interior#1{\mathrm{int}\, #1} \xdef\proj{\Pi} \xdef\epi#1{\mathrm{epi}\, #1} \xdef\grad#1{\mathrm{grad}\, #1} \xdef\gradT#1{\mathrm{grad}^T #1} \xdef\gradx#1{\mathrm{grad}_x #1} \xdef\hess#1{\nabla^2\, #1} \xdef\hessx#1{\nabla^2_x #1} \xdef\jacobx#1{D_x #1} \xdef\jacob#1{D #1} \xdef\subdif#1{\partial #1} \xdef\co#1{\mathrm{co}\, #1} \xdef\iter#1{^{[#1]}} \xdef\str{^*} \xdef\spv{\mcal V} \xdef\civ{\mcal U} \xdef\other#1{\hat{#1}} \xdef\xx{\vv x} \xdef\yy{\vv y} \xdef\partDiff#1{\frac{\partial}{\partial #1}} \xdef\partDeriv#1#2{\frac{\partial #1}{\partial #2}} \xdef\nPartDeriv#1#2#3{\frac{\partial^{#1} #2}{\partial #3}} \xdef\Div#1{\mathrm{div}\, #1}\xdef\rot#1{\mathrm{rot}\,#1} \xdef\d{\,\mathrm{d}}

Základní pojmy

Připomeňme definici jednoduchého oboru V~\tilde V v R3\R^3 (Definice 23 v prezentacích), což je množina, která je sjednocením jednoduchých oborů vzhledem ke všem osám, přičemž jednoduchý obor VV vzhledem k např. ose zz definujeme jako V={[x,y,z]∈R3∣[x,y,z]∈M,g(x,y)≤z≤h(x,y)}, V = \set{[x,y,z] \in \R^3 \mid [x,y,z] \in M, g(x,y) \leq z \leq h(x,y)}, kde M⊆R3M \subseteq \R^3 je množina v rovině, která je omezená uzavřenou jednoduchou křivkou CC.

Jednoduchá křivka neprotíná sama sebe.

Definice ZD.1\D{ZD.1} (nabla operátor)

Hamiltonův nabla operátor definujeme v R2\R^2 jako ∇:=(∂∂x,∂∂y), \nabla := \brackets{\partDiff x, \partDiff y}, z čehož dostáváme, že funkci f:R2→Rf : \R^2 \to \R přiřazuje vektorové pole ∇f=grad f=(∂f∂x,∂f∂y). \nabla f = \grad f = \brackets{ \partDeriv f x, \partDeriv f y}. Obdobně bychom jej definovali pro Rn\R^n.

Hamiltonův operátor ∇\nabla aplikovaný na vektorové pole F\vv F v bodě [x,y][x,y] si můžeme představit jako změny F(x,y)↦F(x~,y~)\vv F(x,y) \mapsto \vv F(\tilde x, \tilde y) při malém posunutí [x,y]↦[x~,y~][x,y] \mapsto [\tilde x, \tilde y]. Potom skalární součin vektorového pole s tímto operátorem pak dává v jistém smyslu "průměr" jak je změna vektorového pole rovnoběžná se zmíněným malým posunem. Naopak vektorový součin těchto dvou členů dává "průměrnou" míru kolmosti změny vektorového pole a malé změny zkoumaného bodu.

Pro lepší intuici doporučuji toto video.

Uveďme jako poznámku, že operátor ∇∘∇=∇2=Δ\nabla \circ \nabla = \nabla^2 = \Delta se nazývá Laplaceův operátor a pro skalární funkci ff má tvar Δf=∂2f∂x2+∂2f∂y2 \Delta f = \nPartDeriv{2}{f}{x^2} + \nPartDeriv{2}{f}{y^2}

Nabla operátor aplikovaný na vektorovou funkci F:R2→R2\vv F : \R^2 \to \R^2 (tj. vektorové pole) dává Jakobiho matici ∇F=(∂F1∂x∂F1∂y∂F2∂x∂F2∂y)\nabla \vv F = \mtr{\partDeriv {\vv F_1} x & \partDeriv {\vv F_1} y \\ \partDeriv{\vv F_2} x & \partDeriv{\vv F_2} y}

Definice ZD.2\D{ZD.2} (divergence)

Nechť máme vektorovou funkci F(x,y)=(P(x,y),Q(x,y))\vv F(x,y) = (P(x,y), Q(x,y)), kde funkce P,Q:R2→RP,Q: \R^2 \to \R jsou spojitě diferencovatelné.

Tedy jsou spojité spolu se svými prvními parciálními derivacemi

Pak s použitím definice ZD.1\tagDe{ZD.1} označíme divergenci vektorového pole jako funkci div :R2→R\Div{} : \R^2 \to \R definovanou předpisem div F=⟨∇,F⟩=∂P∂x+∂Q∂y=Px+Qy. \Div {\vv F} = \scal {\nabla} {\vv F} = \partDeriv P x + \partDeriv Q y = P_x + Q_y. Obdobně bychom divergenci definovali pro vektorové pole v Rn\R^n.

Dále si uvědomme, že divergence uvádá "poměr" přítoku a odtoku vektorového pole v daném bodě. To jest, je-li div F(x,y)>0\Div {\vv F}(x,y) > 0, pak v bodě [x,y][x,y] více vektorové odtéká, než je do toho bodu přítok. Analogicky pro situaci div F(x,y)<0\Div {\vv F}(x,y) < 0.

V analogii s kapalinami by to byl bod, ze kterého kapalina více odtéká, než do něj přitéka - tj. v tomto bodě vzniká kapalina.

Má-li vektorové pole charakterizující nějakou kapalinu pozitivní divergenci, potom by se v něm skrvny (např. ropná skrvna v oceánu) zvětšovaly postupem času

Obdobně můžeme zapsat i totální diferenciál funkce f:Rn→Rf:\R^n \to \R  df=⟨∇f, dx⟩=∂f∂x1 dx1+∂f∂x2 dx2+⋯+∂f∂xn dxn \d f = \scal {\nabla f} {\d \vv x} = \partDeriv{f}{x_1} \d x_1 + \partDeriv{f}{x_2} \d x_2 + \dots + \partDeriv{f}{x_n} \d x_n

Definice ZD.3\D{ZD.3} (zřídlovost)

Vektorové pole F\vv F nazveme nezřídlové, pokud pro každý jeho bod [x,y][x,y] platí div F(x,y)=0. \Div {\vv F}(x,y) = 0. V opačném případě jej nazveme zřídlové.

Definice ZD.4\D{ZD.4} (rotace, curl)

Nechť máme vektorovou funkci F(x,y,z)=(P(x,y,z),Q(x,y,z),R(x,y,z))\vv F(x,y,z) = (P(x,y,z), Q(x,y,z), R(x,y,z)), kde funkce P,Q,R:R3→RP,Q,R: \R^3 \to \R jsou spojitě diferencovatelné.

Pak s použitím definice ZD.1\tagDe{ZD.1} označíme rotaci vektorové pole jako funkci rot :R3→R3\rot{} :\R^3 \to \R^3 s předpisem rot F=∇×F=(Ry−Qz,Pz−Rx,Qx−Py) \rot{\vv F} = \nabla \times \vv F = \brackets{R_y - Q_z, P_z - R_x, Q_x - P_y}

Pro dvourozměrné vektorové pole F:R2→R2\vv F : \R^2 \to \R^2 pak uvažujeme rotaci jako rot :R3→R3\rot{} : \R^3 \to \R^3 s 3. vstupní souřadnicí vždy nulovou a platí rot F=(0,0,Qx−Py) \rot{\vv F} = (0, 0, Q_x - P_y)

Zde je důležité si uvědomit, že ačkoliv pracujeme s 2D vektorovým polem, jeho rotace bude ležet ve 3. dimenzi, neboť musí být kolmá na jak na ∇\nabla, tak i na vektorové pole F\vv F.

Rotace rot F(x,y)\rot{\vv F}(x,y) udává lokální míru rotace v bodě [x,y][x,y] a je-li nulová, pak takové pole nazveme nevírové.

Je-li rotace rot F>0\rot{\vv F} > 0 vektorového pole F\vv F, pak se tato rotace děje proti směru hodinových ručiček z pohledu kladně orientovaného normálního vektoru (osy zz pro F:R2→R2\vv F: \R^2 \to \R^2).

Lemma ZT.1\D{ZT.1} (vlastnosti rotace a divergence)

Nechť máme funkci f:Rn→Rf: \R^n \to \R a vektorovou funkci F(x)=(P1(x),…,Pn(x))\vv F(\vv x) = (P_1(\vv x), \dots, P_n(\vv x)), kde funkce P1,…,Pn:Rn→RP_1, \dots, P_n: \R^n \to \R jsou spojitě diferencovatelné. Pak platí

  1. rot grad f=0\rot{\grad f} = \vv 0
  2. div rot F=0\Div{\rot{\vv F}} = 0

Důkaz:
Důkaz provedeme pro každou část zvlášť. Pro první rovnost jistě platí rot grad f=∇×grad f=∇×∇f, \rot{\grad f} = \nabla \times \grad f = \nabla \times \nabla f, přičemž si zde můžeme uvědomit, že ∇f\nabla f je de facto lineární násobek operátoru ∇\nabla, tedy ∇\nabla a ∇f\nabla f jsou lineárně závislé. Z tohoto plyne, že jejich vektorový součin je nulový vektor. Více rigorózně tento důkaz provedeme v R3\R^3 následovně rot grad f=∇×grad f=∇×(∂f∂x,∂f∂y,∂f∂z)=(∂2f∂zy−∂2f∂yz,∂2f∂zx−∂2f∂xz,∂2f∂yx−∂2f∂xy)=0, \begin{aligned} \rot{\grad f} &= \nabla \times \grad f = \nabla \times \brackets{\partDeriv{f}{x}, \partDeriv{f}{y}, \partDeriv{f}{z}} \\ &= \brackets{ \nPartDeriv{2}{f}{zy} - \nPartDeriv{2}{f}{yz}, \nPartDeriv{2}{f}{zx} - \nPartDeriv{2}{f}{xz}, \nPartDeriv{2}{f}{yx} - \nPartDeriv{2}{f}{xy} } \\ &= \vv 0, \end{aligned} za předpokladu, že ff je dostatečně hladká. V Rn\R^n by se důkaz vedl obdobně.
Dokažme nyní druhou část tohoto lemmatu. Jistě div rot F=⟨∇,rot F⟩=⟨∇,∇×F⟩, \Div{\rot{\vv F}} = \scal {\nabla} {\rot \vv F} = \scal {\nabla} {\nabla \times \vv F}, chápeme-li nyní ∇\nabla jako vektor, pak z definice vektorového součinu je ∇×F⊥∇  ⟹  ⟨∇,∇×F⟩=0\nabla \times \vv F \perp \nabla \implies \scal {\nabla} {\nabla \times \vv F} = 0. ■\blacksquare

Definice ZD.5\D{ZD.5} (křivkový integrál 2. druhu)

Uvažujme vektorové pole F:R2→R2\vv F : \R^2 \to \R^2 a křivku CC charakterizovanou parametrizací t∈[a,b],x=φ(t),y=ψ(t)t \in [a,b], x = \vf(t), y = \psi(t). Potom integrál ∫C⟨F, dx⟩=∫C⟨F, dl⃗⟩=∫C⟨F,t⃗⟩ dt, \int_C \scal{\vv F} {\d \vv x} = \int_C \scal {\vv F} {\d \vec{l}} = \int_C \scal {\vv F} {\vec t} \d t, kde  dx= dl⃗=( dx, dy)\d \vv x = \d \vec{l} = (\d x, \d y) a t⃗=(φ′,ψ′)\vec t = (\vf', \psi'), nazveme křivkový integrál 2. druhu.

Křivkovým integrálem 2. druhu v jakémsi smyslu zobecňujeme koncept "práce" (z fyziky), přičemž standardně jsme zvyklí na vztah W=F⋅dW = F \cdot d, kde dd je délka trajektorie a FF síla působící na těleso posunující ho po zmíněné trajektorii. Představit si můžeme například šikmou plochu, viz obrázek.

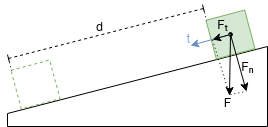
V této situaci gravitační pole působící silou F⃗\vec F vykoná práci pouze části síly FF, která je tečná (v tomto případě rovnoběžná) ke směru pohybu. Tato tečná část je označena F⃗t\vec F_t a jistě platí F⃗t=⟨F⃗,t⃗⟩\vec F_t = \scal{\vec{F}} {\vec {t}} a taktéž W=∣F⃗t∣⋅d=⟨F⃗,t⃗⟩⋅d W = |\vec F_t| \cdot d = \scal{\vec F} {\vec t} \cdot d To ovšem můžeme zapsat i pomocí křivkového integrálu 2. druhu, který udává

    práci, kterou vykoná vektorové pole při posunu tělesa po trajektorii
a tedy W=∫C⟨F⃗,t⃗⟩ dt. W = \int_C \scal {\vec F} {\vec t} \d t.
Definice ZD.6\D{ZD.6} (plošný integrál 2. druhu)

Uvažujme vektorové pole F=(P(x,y,z),Q(x,y,z),R(x,y,z)):R3→R3\vv F = (P(x,y,z),Q(x,y,z),R(x,y,z)) : \R^3 \to \R^3 a plochu SS. Potom ∬S⟨F,n⃗⟩ dS=∬SP(x,y,z) dy dz+Q(x,y,z) dx dz+R(x,y,z) dx dy, \iint_S \scal {\vv F} {\vec{n}} \d S = \iint_S P(x,y,z) \d y \d z + Q(x,y,z) \d x \d z + R(x,y,z) \d x \d y, kde n⃗\vec n je normálový vektor plochy SS, nazýváme plošný integrál 2. druhu.

Plošný integrál 2. druhu nám udává průtok (flux) vektorového pole F\vv F skrze plochu SS, který v každém bodě této plochy počítáme jako skalární součin normály n⃗\vec{n} k ploše SS a vektorového pole F\vv F (což nám dá, jak "velká část" F\vv F směřuje ve směru normály n⃗\vec{n} a tedy protíká onou plochou SS)

Důležité vlastnosti

Věta VT.1\D{VT.1} (Gaussova-Ostrogradského věta/Gauss divergence theorem)

Zformulujme tuto větu prvně slovně, poté i s podmínkami rigorózně:
Průtok vektorového pole F\vv F skrze ohraničenou plochu SS je roven integrálu z divergence div F\Div{\vv F} přes celý objem VV, který plocha SS ohraničuje.

Nechť VV je jednoduchý obor v R3\R^3, F:R3→R3\vv F : \R^3 \to \R^3 je vektorové pole se spojitě diferencovatelnými složkami v každé proměnné a nechť SS je ohraničená plocha ohraničující VV orientovaná ve směru vnější normály. Pak platí ∬S⟨F,n⃗⟩ dS=∭Vdiv F dV \iint_S \scal{\vv F} {\vec{n}} \d S = \iiint_V \Div{\vv F} \d V

Zde si uvědomme, že

  • je-li kapalina nestačitelná (samovolně nemizí/nevzníká, tedy div F=0\Div{\vv F} = 0), potom stejná část "přiteče" do libovolné oblasti, jako z ní odteče
  • stejně tak, točí-li se kapalina (vektorové pole F\vv F) pouze v rámci této oblasti (tedy div F\Div{\vv F} je opět nulový), pak jistě neproudí skrze plochu SS

Abychom pochopili, proč můžeme průtok spočítat přes divergenci v celém objemu, rozdělme si objem VV uzavřený plochou SS na malé obdélníčky (kvádříky v R3\R^3) a spočítejme divergenci v těchto obdélnících (na obrázku jsou znázorněny všechny divergence kladné). Při dostatečně jemném dělení a spojitosti vektorového pole F\vv F zjistíme, že divergence mezi sousedícími stěnami se odečtou (znázorněno červeně) a zbudou nám pouze divergebce v "okrajovém pásu" (aka plocha SS) mířící ven z VV (znázorněny modře).

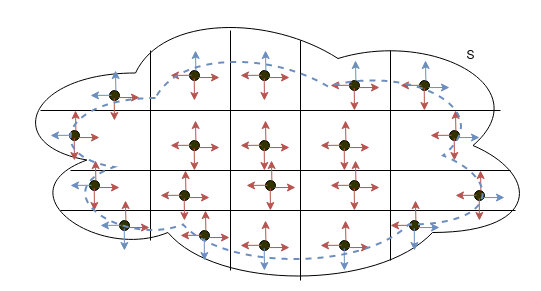
Poznamenejme, že znaménko průtoku dovnitř plochy SS je opačné, než znaménko průtoku vně této plochy. Aneb tuto větu můžeme interpretovat tak, že pokud dohromady (skrze integrál) uvnitř VV (respektive SS) nevzniká ani nemizí žádná kapalina (vektorové pole F\vv F), pak průtok skrze plochu SS musí být nulový (při znaménkové konvenci řečené výše).

Množina G⊆R2G \subseteq \R^2 je jednoduše souvislá oblast, pokud je GG otevřená, souvislá (libovolné 2 body lze spojit lomenou čarou, která leží v GG) a s každou uzavřenou křivkou leží v GG i vnitřek této křivky.

Aneb každá uzavřená křivka v GG lze spojitě deformovat do bodu, aniž bychom GG opustili.

Věta VT.2\D{VT.2} (Stokesova věta)

Nechť plochu SS, která je omezená ohraničenou křivkou CC tvořící kraj SS, lze rozložit na konečný počet částí, které jsou grafy funkcí proměnných x,yx,y, totéž pro x,zx,z a y,zy,z. Nechť vektorové pole F:S→R3\vv F : S \to \R^3 má spojitě diferencovatelné složky na SS. Dále nechť křivka CC je orientovaná souhlasně s plochou SS. Pak platí ∮C⟨F, dx⟩=∬S⟨rot F,n⃗⟩ dS \oint_C \scal{\vv F}{\d \vv x} = \iint_S \scal{\rot{\vv F}}{\vec n} \d S nebo ekvivalentně ∮C⟨F, dl⃗⟩=∬S⟨rot F, dS⃗⟩ \oint_C \scal{\vv F}{\d \vec l} = \iint_S \scal{\rot{\vv F}}{\d \vec S}

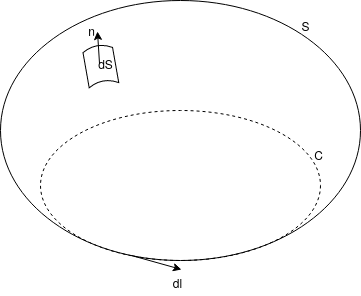
Geometrická odůvodnění si ukážeme na jednodušší variantě - na Greenově větě VT.3\tagDe{VT.3}.

Věta VT.3\D{VT.3} (Greenova věta)

Greenova věta je speciální případ Stokesovy věty VT.2\tagDe{VT.2} pro plochu SS, zde značenou jako GG, jakožto rovinu.

Nechť GG je jednoduše souvislá oblast v rovině, CC je uzavřená, kladně orientovaná (proti směru hod. ručiček) křivka v GG. Dále nechť F:R2→R2\vv F : \R^2 \to \R^2 je vektorové pole se spojitě diferencovatelnými složkami na uzávěru G‾\overline G. Pak platí ∮C⟨F, dx⟩=∬Drot F dx dy⏞ dD, \oint_C \scal{\vv F}{\d \vv x} = \iint_D \rot {\vv F} \overbrace{\d x \d y}^{\d D}, kde DD je část množiny GG omezená křivkou CC a  dl⃗= dx=( dx, dy)\d \vec{l} = \d \vv x = (\d x, \d y) udává tečnu ke křivce CC v daném bodě.

Opět tuto větu odůvodníme podobným argumentem jako u Gaussovy věty VT.1\tagDe{VT.1}, tj. tentokrát plochu SS rozdělíme na obdélníčky, ve kterých určíme rotaci vektorového pole rot F\rot{\vv F}. Zjemňujeme-li toto dělení, všimneme si, že sousedí-li 2 obdélníčky a mají stejně orientovanou rotaci, pak se na sdílené straně "potkají 2 protichůdné směry" a celkem se rotace "odečte". Tímto nám opět zbude pouze rotace na okraji oblasti GG, tedy křivka CC, při které je rotace tečná ke křivce CC - to je ale přesně integrál skalárního součinu vektorového pole F\vv F a malého tečného kroku na křivce CC, tj. dl⃗d \vec{l}.

Back to top