Hry v rozšířené formě (poziční hry)
$$ \xdef\scal#1#2{\langle #1, #2 \rangle} \xdef\norm#1{\left\lVert #1 \right\rVert} \xdef\dist{\rho} \xdef\and{\&}\xdef\AND{\quad \and \quad}\xdef\brackets#1{\left\{ #1 \right\}} \xdef\parc#1#2{\frac {\partial #1}{\partial #2}} \xdef\mtr#1{\begin{pmatrix}#1\end{pmatrix}} \xdef\bm#1{\boldsymbol{#1}} \xdef\mcal#1{\mathcal{#1}} \xdef\vv#1{\mathbf{#1}}\xdef\vvp#1{\pmb{#1}} \xdef\ve{\varepsilon} \xdef\l{\lambda} \xdef\th{\vartheta} \xdef\a{\alpha} \xdef\vf{\varphi} \xdef\Tagged#1{(\text{#1})} \xdef\tagged*#1{\text{#1}} \xdef\tagEqHere#1#2{\href{#2\#eq-#1}{(\text{#1})}} \xdef\tagDeHere#1#2{\href{#2\#de-#1}{\text{#1}}} \xdef\tagEq#1{\href{\#eq-#1}{(\text{#1})}} \xdef\tagDe#1{\href{\#de-#1}{\text{#1}}} \xdef\T#1{\htmlId{eq-#1}{#1}} \xdef\D#1{\htmlId{de-#1}{\vv{#1}}} \xdef\conv#1{\mathrm{conv}\, #1} \xdef\cone#1{\mathrm{cone}\, #1} \xdef\aff#1{\mathrm{aff}\, #1} \xdef\lin#1{\mathrm{Lin}\, #1} \xdef\span#1{\mathrm{span}\, #1} \xdef\O{\mathcal O} \xdef\ri#1{\mathrm{ri}\, #1} \xdef\rd#1{\mathrm{r}\partial\, #1} \xdef\interior#1{\mathrm{int}\, #1} \xdef\proj{\Pi} \xdef\epi#1{\mathrm{epi}\, #1} \xdef\grad#1{\mathrm{grad}\, #1} \xdef\gradT#1{\mathrm{grad}^T #1} \xdef\gradx#1{\mathrm{grad}_x #1} \xdef\hess#1{\nabla^2\, #1} \xdef\hessx#1{\nabla^2_x #1} \xdef\jacobx#1{D_x #1} \xdef\jacob#1{D #1} \xdef\subdif#1{\partial #1} \xdef\co#1{\mathrm{co}\, #1} \xdef\iter#1{^{[#1]}} \xdef\str{^*} \xdef\spv{\mcal V} \xdef\civ{\mcal U} \xdef\other#1{\hat{#1}} \xdef\xx{\vv x} \xdef\yy{\vv y} $$
Také lze nazývat tahové hry
Definice $\D{HvRF}$
Nechť $N$ je množina hračů, $H$ množina historií
- prázdná posloupnost $\ve \in H$
- $(a^k)_ {k = 1}^K, K \in \N \cup \set{\infty}$ je historie $\implies (a^k)_ {k = 1}^L, L < K$ je historie
- máme-li $(a^k)_ {k = 1}^\infty$ a víme, že $\forall L < \infty : (a_k)_ {k = 1}^L$ je historie, pak i $(a^k)_ {k = 1}^\infty$ je historie
Dále nechť $P$ je tahová funkce, $P : H' \to N$ (nebo také $P : H' \to \mcal P(N)$), kde $H' = H - Z$, $Z$ jsou terminální historie, což jsou maximální posloupnosti v $H$ (ty, které neumíme dále rozšířit).
Pak výherní funkce má tvar $u_i : Z \to \R$ nebo může být zadáno pouze preferenční uspořádání $\prec_i$ na $Z$
Příklad
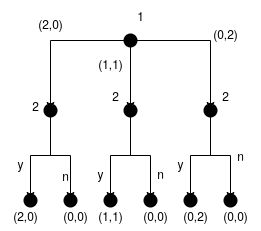
Zde $N = \set{1,2}, P(\ve) = 1$ a $$ P((0,2)) = P((1,1)) = P((2,0)) = 2 $$ a také $u_1((1,1), y) = 1$. Množina historí má tvar $$ H = \set{\ve, (2,0), (1,1), (0,2), ((2,0), y), ((2,0), n), \dots} $$
Strategie pro prvního hráče $$ X =\set{(2,0), (1,1), (0,2)} $$ a pro druhého hráče $$ Y = \set{(2,0), y), (2,0), n), \dots} $$
Obecně zapsáno strategie pro $i$-tého hráče je množina $$ X_i = \set{f : \bar H \to H \mid \bar H = \set{\bar h \in H \mid P(\bar h) = i}, \bar h \text{ je podposloupnost } f(\bar h) \text{ bez posledního členu}} $$
Nashova rovnováha:
Máme výherní funkci
$$
u_i(\bar f _i, f _{\hat i}) \geq u_i(f _i, f _{\hat i}),
$$
tj. $i$ volí nejlepší odpověď na $f_{\hat i}$. Pak
$$
(\bar f_i)_{i \in N}
$$
je rovnováha.
Dále definujme podhru hry $(N, H, P, (X _i) _{i \in N}, (u _i) _{i \in N})$ jako $$ (N, H \mid_h, P\mid_h, (X _i \mid_h) _{i \in N}, (u _i\mid_h) _{i \in N}), $$ kde $h \in H$ pevná historie a $h' \in H \mid_h \iff (h, h') \in H$. Dále
- $P\mid_h (h') = P(h, h')$
- $f' \in X_i \mid_h \iff (\exists f \in X_i) (\forall \bar h \in \bar H \mid_h) \quad (h, f'(\bar h)) = f(h, \bar h)$
- $u_i \mid_h (h') = u_i (h, h')$
Situace $(f_i)_{i \in N}$ je perfektní podherní rovnováha (PPR), je-li takto zvolené $(f_i \mid_h)_{i \in N}$ (Nashovou) rovnováhou pro každou historii $h$.
Pokračování příkladu
Rovnováha $$ \left((1,1), \begin{matrix} (2,0) \mapsto ((2,0), n) \ (1,1) \mapsto ((1,1), y) \ (0,2) \mapsto ((0,2), n) \end{matrix} \right), $$ což ale není perfektní podherní rovhována, neboť se zde $(0,2) \mapsto ((0,2), n$ rozhodl špatně, jinak řečeno $$ H \mid_h \qquad u_2((0,2), n) < u_2((0,2), y) $$
Tedy perfektní podherní rovnováha je v tomto případě $$ \left((1,1), \begin{matrix} (2,0) \mapsto ((2,0), n) \ (1,1) \mapsto ((1,1), y) \ (0,2) \mapsto ((0,2), y) \end{matrix} \right), $$ ale také $$ \left((1,1), \begin{matrix} (2,0) \mapsto ((2,0), y) \ (1,1) \mapsto ((1,1), y) \ (0,2) \mapsto ((0,2), y) \end{matrix} \right) $$
Lemma $\D{L1}$
Nechť $G = (N, H, P, \mcal X, \mcal U)$ je hra v rozšířené formě s konečným horizontem (všechny historie jsou konečné). Pak situace $(f_i)_{i \in N}$ je PPR $$ \iff \forall i \in N, \; \forall h \in H, \; P(h) = i \implies u_i((f_i \mid_h)_{i \in N}) \geq u_i(\tilde f_i, (f_j \mid_h)_{j \in \hat i}), $$ kde $\tilde f_i \in H \mid_h$ se liší od $f_i \mid_h$ pouze akcemi po $h$
Věta $\D{V1}$
Je-li $G = (N, H, P, \mcal X, \mcal U)$ konečná hra v rozšířené formě (tj. má konečný horizont a v každém vrcholu se rozhodujeme z konečně mnoha variant, tj. $H$ je konečná), pak existuje PPR*.
Dále tuto tématiku rozšiřují tzv. folkové věty.
Příklad: Stonožka
Máme 2 hráče $N = \set{1,2}$
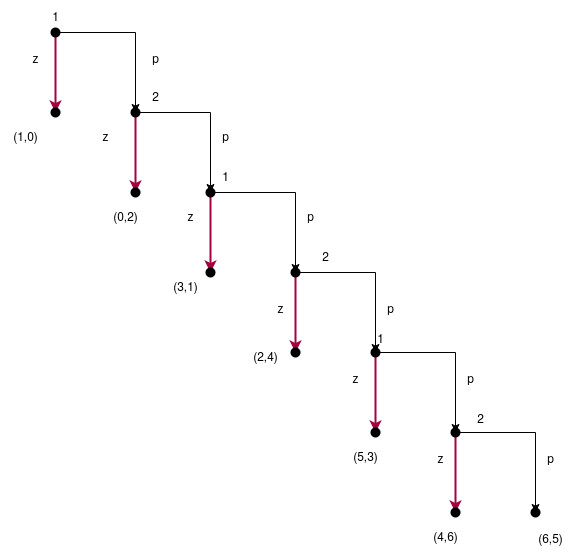
A $$ f_1 = \begin{pmatrix} \ve \mapsto (z) \ (p,p) \mapsto (p,p,z) \ (p,p,p,p) \mapsto (p,p,p,p,z) \end{pmatrix} $$ a $f_2 = (\dots)$ analogicky.
Příklad: Dražba s placením

Tedy $$ \overbrace{ \mtr{ (-\infty, -\infty) & (4,0) \ (0,5) & (0,5) } }^{(p,\dots, p), \quad (z, \dots, z)}, $$ kde $(4,0)$ je rovnováha a $(0,5)$
