Skip to main content

Hry s neúplnou informací

$$ \xdef\scal#1#2{\langle #1, #2 \rangle} \xdef\norm#1{\left\lVert #1 \right\rVert} \xdef\dist{\rho} \xdef\and{\&}\xdef\AND{\quad \and \quad}\xdef\brackets#1{\left\{ #1 \right\}} \xdef\parc#1#2{\frac {\partial #1}{\partial #2}} \xdef\mtr#1{\begin{pmatrix}#1\end{pmatrix}} \xdef\bm#1{\boldsymbol{#1}} \xdef\mcal#1{\mathcal{#1}} \xdef\vv#1{\mathbf{#1}}\xdef\vvp#1{\pmb{#1}} \xdef\ve{\varepsilon} \xdef\l{\lambda} \xdef\th{\vartheta} \xdef\a{\alpha} \xdef\vf{\varphi} \xdef\Tagged#1{(\text{#1})} \xdef\tagged*#1{\text{#1}} \xdef\tagEqHere#1#2{\href{#2\#eq-#1}{(\text{#1})}} \xdef\tagDeHere#1#2{\href{#2\#de-#1}{\text{#1}}} \xdef\tagEq#1{\href{\#eq-#1}{(\text{#1})}} \xdef\tagDe#1{\href{\#de-#1}{\text{#1}}} \xdef\T#1{\htmlId{eq-#1}{#1}} \xdef\D#1{\htmlId{de-#1}{\vv{#1}}} \xdef\conv#1{\mathrm{conv}\, #1} \xdef\cone#1{\mathrm{cone}\, #1} \xdef\aff#1{\mathrm{aff}\, #1} \xdef\lin#1{\mathrm{Lin}\, #1} \xdef\span#1{\mathrm{span}\, #1} \xdef\O{\mathcal O} \xdef\ri#1{\mathrm{ri}\, #1} \xdef\rd#1{\mathrm{r}\partial\, #1} \xdef\interior#1{\mathrm{int}\, #1} \xdef\proj{\Pi} \xdef\epi#1{\mathrm{epi}\, #1} \xdef\grad#1{\mathrm{grad}\, #1} \xdef\gradT#1{\mathrm{grad}^T #1} \xdef\gradx#1{\mathrm{grad}_x #1} \xdef\hess#1{\nabla^2\, #1} \xdef\hessx#1{\nabla^2_x #1} \xdef\jacobx#1{D_x #1} \xdef\jacob#1{D #1} \xdef\subdif#1{\partial #1} \xdef\co#1{\mathrm{co}\, #1} \xdef\iter#1{^{[#1]}} \xdef\str{^*} \xdef\spv{\mcal V} \xdef\civ{\mcal U} \xdef\other#1{\hat{#1}} \xdef\xx{\vv x} \xdef\yy{\vv y} $$

Znalost

Nechť $\Omega$ označuje množinu stavů. Mějme informační funkci $P$, přičemž $P(\omega) \subseteq \Omega$

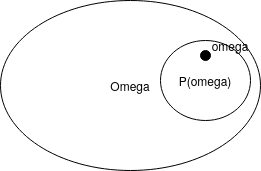
a máme 2 axiomy $$ \forall \omega \in \Omega \quad \omega \in P(\omega) \tag{\T{P1}} $$ a $$ \omega' \in P(\omega) \implies P(\omega') = P(\omega) \tag{\T{P2}}, $$ přičemž z $\tagEq{P1},\tagEq{P2}$ plyne, že $P$ vytváří rozklad na $\Omega$.

Dále definujme $K$ znalostní funkci a $E \subseteq \Omega$ událost a platí $$ K(E) = \set{\omega \in \Omega \mid P(\omega) \subseteq E}, $$ splňující

  1. $$K(\Omega) = \Omega \tag{\T{K1}}$$
  2. $$E \subseteq F \implies K(E) \subseteq K(F) \tag{\T{K2}}$$

  3. $$K(E) \cap K(F) = K(E \cap F) \tag{\T{K3}}$$
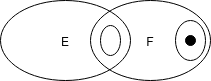
  1. $$K(E) \subseteq E \tag{\T{K4}}$$
  2. $$K(K(E)) = K(E) \tag{\T{K5}}$$
  3. (axiom moudrosti)
    $$\Omega \setminus K(E) = K(\Omega \setminus K(E)) \tag{\T{K6}}$$

Příklad - Hádání barvy klobouku

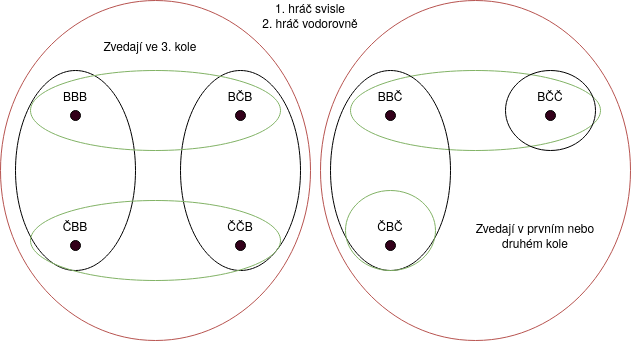
Pro začátek uvažujme 3 hráče, každý dostane černý nebo bílý klobouk, přičemž jeho barvu nezná. Hráči ví, že minimálně jeden klobouk je bílý. Hráči kteří odhadnou, jakou barvu má jejich klobouk, zvednou ruku a hraje dokud to všichni neví.

Možné situace

  • BČČ $\implies$ $\uparrow$?? $\implies$ (pokud by 1. nevěděl, že má jediný bílý, nezvedal by ruku) KONEC
  • BBČ $\implies$ ??? $\implies$ (bílý si řekne, druhý bílý nezvedl ruku, tedy já musím být taky bílý) $\uparrow$$\uparrow$? $\implies$ (černý nic neví, ale ostatní to už věděli, takže musí mít černý) KONEC
  • BBB $\implies$ ??? $\implies$ ??? $\implies$ (nikdo nic neví, tedy musí mít někdo bílý klobouk) KONEC

Jistě $$ \Omega = \set{c \in \set{\text{B}, \text{Č}}^n \mid \exists i \in N : c(i) = B} $$ a označme $P^i_j$ informační funkci $i$-tého hráče v $j$-tém kole ($j = 1,2,\dots$)

V případě BČČ je $P_1^1 (\text{BČČ}) = \set{\text{BČČ}}$, ale v $P_1^1(\text{BBČ}) = \set{\text{BBČ}, \text{ČBČ}}$

Dále označme $E_i$ jako událost, ve které $i$-tý hráč dozvěděl svoji barvu a tedy $|E_i| = 1$. Nyní nechť $$ F^k = \set{c ; \; |\set{c(i) = B}| = k} $$

Potom $P_i^2(c) = P_i^1(c) - F^1$. V našem případě $$ F^1 = \set{\text{BČČ}, \text{ČBČ}, \text{ČČB}}, F^2 = \set{\text{BBČ}, \text{BČB}, \text{ČBB}}, $$ proto $$ P_1^1(\text{BBČ}) = \set{\text{BBČ}, \text{ČBČ}} \implies \ P_1^2 = P_1^1(\text{BBČ}), \qquad P^3_1(\text{BBČ}) = \set{\underbrace{\text{ČBČ}}_{\in E_1}} $$

Označme $K_1, K_2$ - znalostní funkce 1. a 2. hráče. Dále $E$ je společnou znalostí ve stavu $\omega$, pokud $$K_1(E), K_2(E), K_1(K_2(E)), K_ 2(K_ 1(E)), K_2(K_1(K_2(E))), K_1(K_2(K_1(E))), \dots$$ obsahuje $\omega$.

Např. $$ P_1 = \set{ \set{\omega_1, \omega_2}, \set{\omega_3, \omega_4, \omega_5}, \set{\omega_6} }, \ P_2 = \set{ \set{\omega_1}, \set{\omega_2, \dots, \omega_5}, \set{\omega_5}, \set{\omega_6} }, \ E = \set{\omega_1, \dots, \omega_4}, $$ pak jistě

  • $K_1(E) = \set{\omega_1, \omega_2}$
  • $K_2(E) = \set{\omega_1, \dots, \omega_4}$
  • $K_1(K_2(E)) = \set{\omega_1, \omega_2}$ a $K_2(K_1(E)) = \set{\omega_1} = K_2(K_1(K_2(E)))$
  • $K_1(K_2(K_1(E)))) = \emptyset$

Událost $F \subseteq \Omega$ je samozřejmá mezi 1. a 2. hráčem, jestliže $\forall \omega \in F : P_i(\omega) \subseteq F$ pro $i = 1, 2$

$E$ je společnou znalostí v $\omega$, polid existuje $F$, $\omega \in F$, samozřejmá pro $i = 1,2$. Např. $$ F = \set{\omega_1, \dots, \omega_5} $$

V příkladu s klobouky

$$ P_1^1 = \set{ \set{BČČ}, \set{BBČ, ČBČ}, \set{BČB, ČČB}, \set{BBB, ČBB} } \ P_2^1 = \set{ \set{ČBČ}, \set{BBČ, BČČ}, \set{ČBB, ČCB}, \set{BBB, BČB} } $$

Back to top