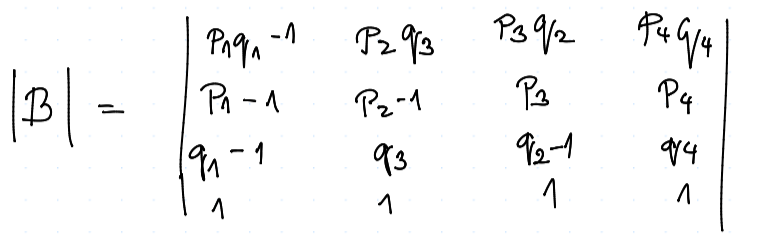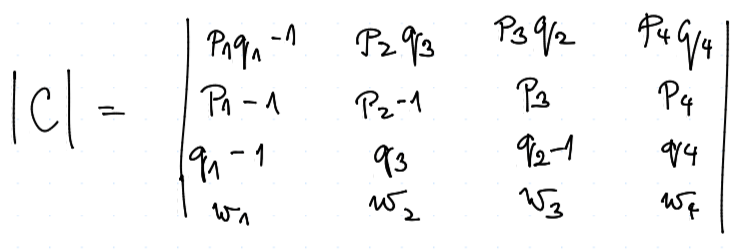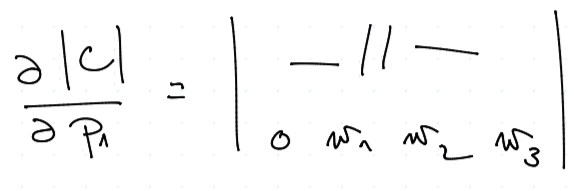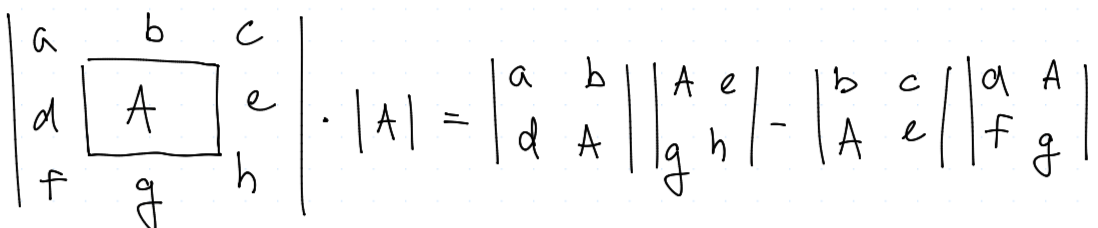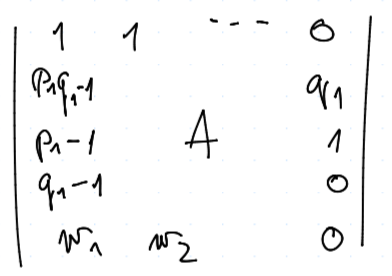5. přednáška

$$\xdef\scal#1#2{\langle #1, #2 \rangle} \xdef\norm#1{\left\lVert #1 \right\rVert} \xdef\dist{\rho} \xdef\and{\&}\xdef\AND{\quad \and \quad}\xdef\brackets#1{\left\{ #1 \right\}} \xdef\parc#1#2{\frac {\partial #1}{\partial #2}} \xdef\mtr#1{\begin{pmatrix}#1\end{pmatrix}} \xdef\nmtr#1{\begin{matrix}#1\end{matrix}} \xdef\bm#1{\boldsymbol{#1}} \xdef\mcal#1{\mathcal{#1}} \xdef\vv#1{\mathbf{#1}}\xdef\vvp#1{\pmb{#1}} \xdef\ve{\varepsilon} \xdef\l{\lambda} \xdef\th{\vartheta} \xdef\a{\alpha} \xdef\vf{\varphi} \xdef\Tagged#1{(\text{#1})} \xdef\tagged*#1{\text{#1}} \xdef\tagEqHere#1#2{\href{#2\#eq-#1}{(\text{#1})}} \xdef\tagDeHere#1#2{\href{#2\#de-#1}{\text{#1}}} \xdef\tagEq#1{\href{\#eq-#1}{(\text{#1})}} \xdef\tagDe#1{\href{\#de-#1}{\text{#1}}} \xdef\T#1{\htmlId{eq-#1}{#1}} \xdef\D#1{\htmlId{de-#1}{\vv{#1}}} \xdef\conv#1{\mathrm{conv}\, #1} \xdef\cone#1{\mathrm{cone}\, #1} \xdef\aff#1{\mathrm{aff}\, #1} \xdef\lin#1{\mathrm{Lin}\, #1} \xdef\span#1{\mathrm{span}\, #1} \xdef\O{\mathcal O} \xdef\ri#1{\mathrm{ri}\, #1} \xdef\rd#1{\mathrm{r}\partial\, #1} \xdef\interior#1{\mathrm{int}\, #1} \xdef\proj{\Pi} \xdef\epi#1{\mathrm{epi}\, #1} \xdef\grad#1{\mathrm{grad}\, #1} \xdef\gradT#1{\mathrm{grad}^T #1} \xdef\gradx#1{\mathrm{grad}_x #1} \xdef\hess#1{\nabla^2\, #1} \xdef\hessx#1{\nabla^2_x #1} \xdef\jacobx#1{D_x #1} \xdef\jacob#1{D #1} \xdef\subdif#1{\partial #1} \xdef\co#1{\mathrm{co}\, #1} \xdef\iter#1{^{[#1]}} \xdef\str{^*} \xdef\spv{\mcal V} \xdef\civ{\mcal U} \xdef\other#1{\hat{#1}}$$

Klasifikace 2x2 her

Předpokládejme, že máme hru $$\mtr{ 0 & a \\ b & 1 },$$ kde $0 \leq a \leq b \leq 1$, což v extrémech odpovídá

0	$a$	$b$	1
0	1	1	1
0	0	0	1
0	0	1	1

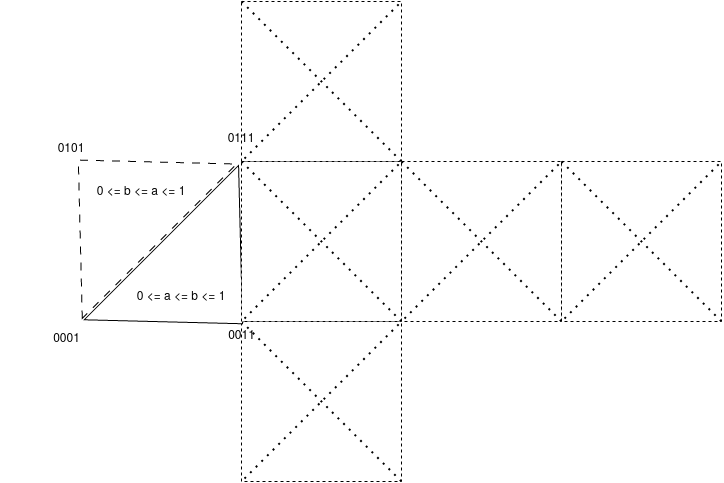
Tady změna krychle odpovídá změně jedné nerovnosti

Opakované hry

Mějme strategii v 1-paměťovém prostředí $(p_0, p_1, p_2, p_3, p_4)$, kde

• $p_0$ - pravděpodobnost spolupráce $S$ na začátku (v 1. kole)
• $p_1$ - pravděpodobnost spolupráce $S$ po $SS$
• $p_2$ - pravděpodobnost spolupráce $S$ po $SZ$
• $p_3$ - pravděpodobnost spolupráce $S$ po $ZS$
• $p_4$ - pravděpodobnost spolupráce $S$ po $ZZ$

$1 - p_i$ je pravděpodobnost zrady $Z$ po $\dots$

A nechť soupeř má strategii $(q_0, q_1, q_2, q_3, q_4)$, přičemž si uvědomme, že ZS pro nás je SZ pro něj apod.

Napišme si výherní matici do řádku do výherního vektoru $$w = \underbrace{(w_1, w_2, w_3, w_4)}_{(SS, SZ, ZS, ZZ)}$$

A pak výhru v $n$-tém kolem dostaneme jako $$(u(p,q))_n = w \cdot \mtr{P_1 \\ \vdots \\ P_4},$$ kde $P_i$ je pravděpodobnost, že hra dospěla do stavu $SS, SZ, ZS, ZZ$

Vektor $\mtr{P_1 \\ \vdots \\ P_4}$ určíme pomocí teorie markovských řetězců. Spočítejme si přechodovou matici $A$ - ta bude mít tvar $$A = \begin{matrix} SS \\ SZ \\ ZS \\ ZZ \end{matrix}\underbrace{\mtr{ p_1 q_1 & p_2 q_3 & p_3 q_2 & p_4 q_4\\ p_1 (1 - q_1) & p_2 (1 - q_3) & p_3 (1 - q_2) & p_4 (1 - q_4) \\ (1-p_1)q_1 & (1 - p_2)q_3 & (1 - p_3) q_2 & (1 - p_4) q_4 \\ (1 - p_1)(1 - q_1) & (1- p_2) (1 - q_3) & (1 - p_3) (1 - q_2) & (1 - p_4) (1 - q_4) }}_{SS, SZ, ZS, ZZ}$$

A pak jistě platí $$P = A^n \mtr{ p_0 q_0 \\ p_0 (1 - q_0) \\ \vdots }$$

Za předpokladu stability se neprojeví počáteční vektor $\mtr{ p_0 q_0 \\ p_0 (1 - q_0) \\ \vdots }$, ale hra dospěje do vektoru $\vv x$ takového, že $A \vv x = \vv x$

Matice $A$ musí být pravděpodobností, tj. suma v každém sloupci musí být 1.

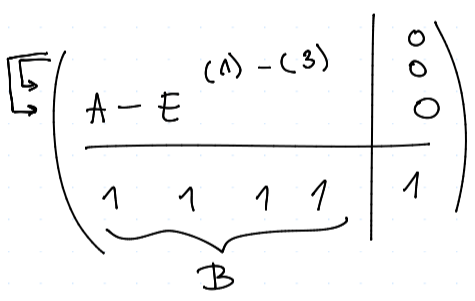
Tento problém řešíme jako $$A \vv x = x \\ (A - I)\vv x = 0,$$ kde $\vv x$ říkáme stacionární vektor (z lingebry dostaneme, že řešení musí jediné až na násobek), který také musí být pravděpodobnostní, tj. $\sum \vv x = 1$.

Rozepišme si $$A- E = \mtr{ p_1 q_1 - 1 & p_2 q_3 & p_3 q_2 & p_4 q_4\\ p_1 (1 - q_1) & p_2 (1 - q_3) - 1 & p_3 (1 - q_2) & p_4 (1 - q_4) \\ (1-p_1)q_1 & (1 - p_2)q_3 & (1 - p_3) q_2 - 1 & (1 - p_4) q_4 \\ (1 - p_1)(1 - q_1) & (1- p_2) (1 - q_3) & (1 - p_3) (1 - q_2) & (1 - p_4) (1 - q_4) - 1 },$$ což řešme pomocí Cramerova pravidla

a tedy $$\vv x_1 = \frac {|B_1|} {|B|}$$

kde $B_1$ je matice, kde jsme 1. sloupec vyměnili za sloupec pravých stran

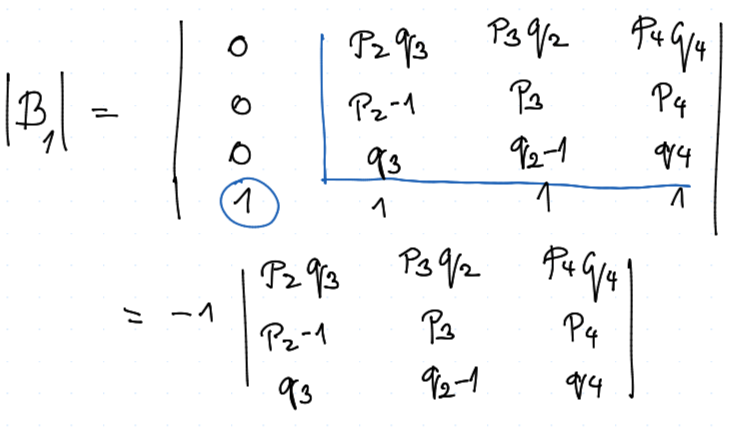
V tuto chvíli, pokud budeme pouze sčítat řádky, tak se nám nemění determinant. Tedy přičtěme 1. řádek z $B$ k tomu 2. a 3., tj.

A proveďme Laplaceův rozvoj podle 1. řádků pro $B_1$

Obdobně bychom postupovali i pro $B_2$

Celkem naše výhra $$u = w_1 \vv x_1 + w_2 \vv x_2 + \dots \\ u = w_1 \frac {|B_1|} {|B|} + w_2 \frac {|B_2|} {|B|} + \dots \\ u = \frac{w_1 |B_1| + w_2 |B_2| + \dots} {|B|},$$ přičemž jmenovatel můžeme vnímat jako Laplaceův rozvoj pro $B$, kde místo vektoru $1$ jsme dali vektor $w$, tj.

Celkem výhru dostaneme jako $$u = \frac {|C|} {|B|}$$

Uvědomme si, že každá proměnná je lineárné v každém z determinantů (vyskytuje se vždy pouze v jednom sloupci), tj. $$u = \frac{\alpha p_i + \beta} {\gamma p_i + \delta}$$

Počítejme optimální vektor $(p_1, \dots, p_4)$, tedy $$\parc u {p_i} = \frac{\alpha(\gamma p_i + \delta) - (\alpha p_i + \beta) \gamma}{(\gamma p_i + \delta)^2} \\ \parc u {p_i} = \frac{\alpha \delta - \beta \gamma}{\underbrace{(\gamma p_i + \delta)^2}_{> 0}}$$

Tedy to znamená, že řešíme znaménko pouze u $\alpha \delta - \beta \gamma$

Tedy se výhra řídí ryze rostoucí, či ryze klesající, funkcí v každém parametru

Celkem nejlepší protihra (odpověď) se realizuje nějakou "rohovou" strategií, tj. volbou $p_i \in \set{0,1}$ (nebo s šumem $\set{\ve, 1 - \ve}$)

Případě, že nám vyjde parciální derivace nulová, tak dostaneme "nerohové strategie", což odpovídá celé jedné stěně hyperkryhclehyperkrychle $[0,1]^4$.

Spočítejme si nyní onu parciální derivaci "pořádně":

Z tohoto dostáváme podle Dasnanotovy-Jacobiho formule

ve smyslu jejího značení $$|A| = \left|\begin{matrix} p_2 q_3 & \dots \\ p_2 - 1 & \dots \\ q_3 & \dots \end{matrix}\right|$$

V této formě to na zkoušce nebude

Speciální strategie v IPD

• ekvalizátor - soupeř si volí $\vv q$ tak, aby $u$ byla konstatní
  • realizuje se lineární závislostí $\mtr{q_1 & q_3 & q_2 - 1 & q_4}, \mtr{1 & 1 & 1 & 1}$ a $\mtr{w_1 & w_2 & w_3 & w_4}$
  • některé determinanty jsou zde nulové
• 0-determinant (ZD-strategie)
  • rozdíl mezi $u$ a $v$ je prohození $w_2$ a $w_2$ (je to symetrická hra)
  • $v$ se liší od $v$ vektorem výher $\bar w = \mtr{w_1 & w_3 & w_2 & w_4}$
  • $$u = \frac {|w|} {|1|}, \qquad v = \frac {|\bar w|} {|1|}$$ a $$\left|\begin{matrix} q_1 & \dots & q_4 \\ 1 & \dots & 4 \\ w_1 & \dots & w_4 \\ w_1 & \searrow \hspace{-10pt}\swarrow & w_4 \end{matrix}\right|$$
  • jsou tzv. vyděračské strategie