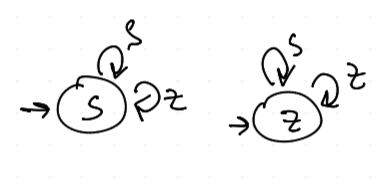4. přednáška
$$ \xdef\scal#1#2{\langle #1, #2 \rangle} \xdef\norm#1{\left\lVert #1 \right\rVert} \xdef\dist{\rho} \xdef\and{\&}\xdef\AND{\quad \and \quad}\xdef\brackets#1{\left\{ #1 \right\}} \xdef\parc#1#2{\frac {\partial #1}{\partial #2}} \xdef\mtr#1{\begin{pmatrix}#1\end{pmatrix}} \xdef\nmtr#1{\begin{matrix}#1\end{matrix}} \xdef\bm#1{\boldsymbol{#1}} \xdef\mcal#1{\mathcal{#1}} \xdef\vv#1{\mathbf{#1}}\xdef\vvp#1{\pmb{#1}} \xdef\ve{\varepsilon} \xdef\l{\lambda} \xdef\th{\vartheta} \xdef\a{\alpha} \xdef\vf{\varphi} \xdef\Tagged#1{(\text{#1})} \xdef\tagged*#1{\text{#1}} \xdef\tagEqHere#1#2{\href{#2\#eq-#1}{(\text{#1})}} \xdef\tagDeHere#1#2{\href{#2\#de-#1}{\text{#1}}} \xdef\tagEq#1{\href{\#eq-#1}{(\text{#1})}} \xdef\tagDe#1{\href{\#de-#1}{\text{#1}}} \xdef\T#1{\htmlId{eq-#1}{#1}} \xdef\D#1{\htmlId{de-#1}{\vv{#1}}} \xdef\conv#1{\mathrm{conv}\, #1} \xdef\cone#1{\mathrm{cone}\, #1} \xdef\aff#1{\mathrm{aff}\, #1} \xdef\lin#1{\mathrm{Lin}\, #1} \xdef\span#1{\mathrm{span}\, #1} \xdef\O{\mathcal O} \xdef\ri#1{\mathrm{ri}\, #1} \xdef\rd#1{\mathrm{r}\partial\, #1} \xdef\interior#1{\mathrm{int}\, #1} \xdef\proj{\Pi} \xdef\epi#1{\mathrm{epi}\, #1} \xdef\grad#1{\mathrm{grad}\, #1} \xdef\gradT#1{\mathrm{grad}^T #1} \xdef\gradx#1{\mathrm{grad}_x #1} \xdef\hess#1{\nabla^2\, #1} \xdef\hessx#1{\nabla^2_x #1} \xdef\jacobx#1{D_x #1} \xdef\jacob#1{D #1} \xdef\subdif#1{\partial #1} \xdef\co#1{\mathrm{co}\, #1} \xdef\iter#1{^{[#1]}} \xdef\str{^*} \xdef\spv{\mcal V} \xdef\civ{\mcal U} \xdef\other#1{\hat{#1}} $$
Opakované hry
Znovu definujme strategii, jako celkový vzorec chování (algoritmus, kterým vybíráme akci pro dané kolo). Akce je výběr pro dané kolo.
Rozdělme si je na
- konečné opakování
- nekonečné opakování
Konečné vězňovo dilema
Mějme matici hry $$ \begin{matrix} \text{spolupracovat} \ \text{zradit} \end{matrix} \mtr{ 2 & 0 \ 3 & 1 } $$
V 1 kolové hře bylo logické zradit
Nyní předpokládejme, že ji budeme hrát $2 \times$:
- Jistě v 2. druhém kole bude výhodné zradit ($ZZ$)
- Jelikož v 2. kole dávalo smysl pouze zradit, tak i v prvním kolem budeme zrazovat, protože 2. kolo stejně nijak neovlivníme
Obecně pro konečné opakování vězňova dilematu vede k výsledku $ZZ$ pro všechna kola
Nekonečné vězňovo dilema
Můžeme interpretovat, že nevíme, které kolo je poslední.
Celkovou výhru si definujme jako:
-
Mějme výhry prvního hráče v $i$-tém kole $$ u_1, u_2, \dots $$ Pak vezmeme částečný průměr, který pošleme do limity, jako výhru, tj. $$ u = \lim_{n \to \infty} \frac {u_1 + \dots + u_n} n $$ Avšak pro například řadu výher $$ 1, 0, \underbrace{1}_ {\frac 1 2}, 0, 0, \underbrace{1}_ {\frac 1 4}, 1, 1, 1, 1, 1, 1, 1, 1, \underbrace{1}_{\frac 3 4}, \dots $$
Tedy částečné průměry nefungují obecně
-
Pomocí disktování
Zaveďme $\delta \in (0,1)$ (diskontní faktor) a pak $$ \bar u_1 = \delta u_1 \ \bar u_2 = \delta^2 u_2 \ \vdots \ \bar u_n = \delta^n u_n $$Tedy v tomto případě mají větší hodnotu "peníze" (výhra), která je teď. Navíc je degradace hry pořád stejná
Velké $\delta$ můžeme interpretovat jako "střadatele"... Pro malé $\delta$ "žije hráč okamžikem" $$ u = \delta u_1 + \delta^2 u_2 + \dots $$ Lze vždy sečíst -
Overtaking
Pro 2 posloupnosti výher $$ u_1, u_2, \dots \ \bar u_1, \bar u_2, \dots $$ Pak řekneme, že $u_i \succ \bar u_i$ pokud $\liminf_{n \to \infty} (u_1 - \bar u_1) + \dots + (u_n - \bar u_n) > 0$Z pohledu psycholgie je pro nás důležitější výsledek "ve většině případů"
Jsou-li strategie hráčů dány konečnými automaty, pak lze výhry sečíst částečným průměrováním.
Vybrané strategie pro vězňovo dilema
Spoušť (Trigger)
Hodí se pro existenční důkazy
Oko za oko (TFT - Tit For Tat)
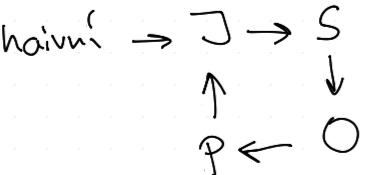
Hrdlička a Jestřáb (Always Cooperate (AllC) / Always Defect (AllD))
Pavlov (pes) (Win Stay Lose Switch - WSLS)
Často zavádíme šum $\ve > 0$ a předpokládáme, že hráč dodrží svou strategii (plán své strategie) s pravděpodobností $1 - \ve$, tj. s pravděpodobností $\ve$ dojde k zahrání opačné akce.
Podívejme se nyní na
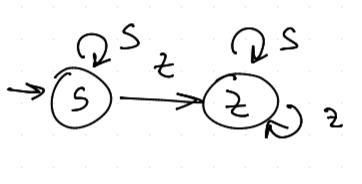
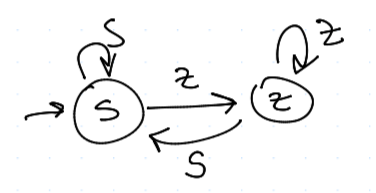
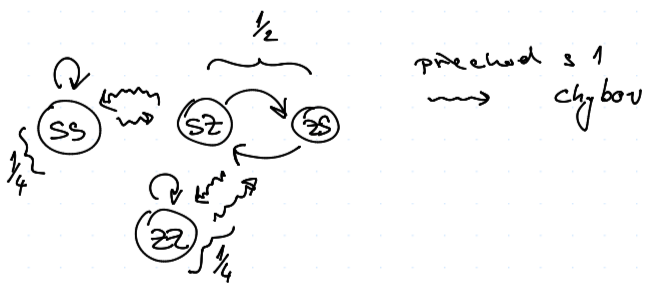
TFT vs. TFT
Možné stavy
Počítejme výhru prvního částečným průměrováním $$ u = \frac 1 4 \cdot 2 + \frac 1 2 \frac {0 + 3} 2 + \frac 1 4 \cdot 1 = \frac 3 2 $$
Oko za oko je trochu moc přísné
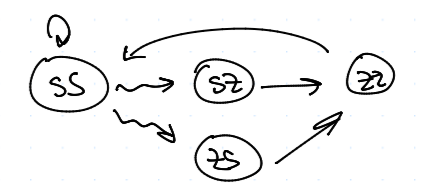
WSLS vs. WSLS
Přičemž $$ u \approx 2 - \ve x $$
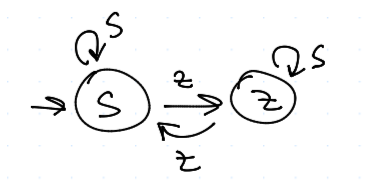
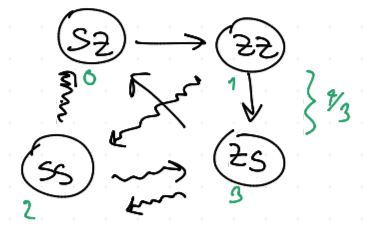
TFT vs. WSLS
Turnaj
| X | S | O | H | J | P | $\sum$ |
| S | $\approx 1$ | $\approx 1$ | $\approx 5/2$ | $\approx 1$ | $\approx 1$ | $\approx \frac {13} 2$ |
| O | ||||||
| H | ||||||
| J | $2$ | |||||
| P | $\frac 1 2$ |
Pokud je hodně "pes" strategií v Turnaji, tak vyhraje, protože spolu dobře spolupracuje
V "evoluční/populační" variantě, tj. necháváme potomky dobrých strategií v turnaji, často vyhraje pes, protože hraje dobře sám se sebou
Strategie se stochastickými přestupy
Šlechetné oko
nebo můžeme udělat novou parametrizaci
- $p_0$ - pravděpodobnost spoluprací na začátku
- $1 - p_0$ - začnu zradou
- $p_1$ - pst. přechodu od SS ke spolupráci
- $p_2$ - pst. přechodu od SZ ke spolupráci
- $p_3$ - pst. přechodu od ZS ke spolupráci
- $p_4$ - pst. přechodu od ZZ ke spolupráci
| $\to$ S | SS $\to$ S | SZ $\to$ S | ZS $\to$ S | ZZ $\to$ S | ||
|---|---|---|---|---|---|---|
| X | $p_0$ | $p_1$ | $p_2$ | $p_3$ | $p_4$ | šum |
| J | 0 | 0 | 0 | 0 | 0 | $(\ve, \ve, \ve, \ve, \ve)$ |
| H | 1 | 1 | 1 | 1 | 1 | $(1 - \ve, \dots)$ |
| S | 1 | 1 | 0 | 0 | 0 | |
| O | 1 | 1 | 0 | 1 | 0 | |
| P | 1 | 1 | 0 | 0 | 1 | |
| ŠO | 1 | 1 | $\frac 1 2$ | 1 | $\frac 1 2$ |
Všechny zmíněme byly tzv. jednopaměťové strategie, tzn. akce vychází pouze z předchozího kola
V Axelrodově turnaji byly i strategie s delší pamětí, ale nebyly moc dobré
V této parametrizaci v evolučním vývoji nastalo
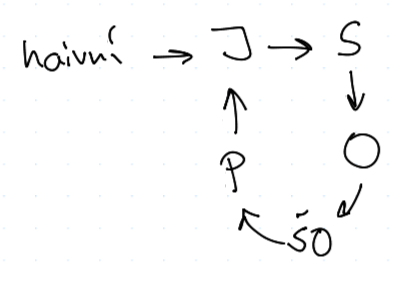
Je to svým způsobem analogie pravděpodobnostního rozšíření, kdy strategie definujeme jako pětice parametrů
Jak dopadne $(p_0, \dots, p_4)$ proti $(q_0, \dots, q_4)$?