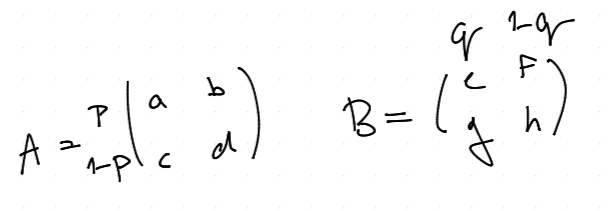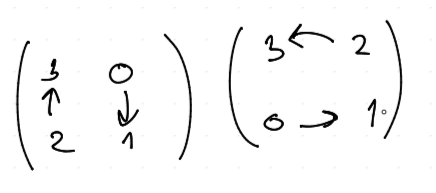3. přednáška

$$ \xdef\scal#1#2{\langle #1, #2 \rangle} \xdef\norm#1{\left\lVert #1 \right\rVert} \xdef\dist{\rho} \xdef\and{\&}\xdef\AND{\quad \and \quad}\xdef\brackets#1{\left\{ #1 \right\}} \xdef\parc#1#2{\frac {\partial #1}{\partial #2}} \xdef\mtr#1{\begin{pmatrix}#1\end{pmatrix}} \xdef\nmtr#1{\begin{matrix}#1\end{matrix}} \xdef\bm#1{\boldsymbol{#1}} \xdef\mcal#1{\mathcal{#1}} \xdef\vv#1{\mathbf{#1}}\xdef\vvp#1{\pmb{#1}} \xdef\ve{\varepsilon} \xdef\l{\lambda} \xdef\th{\vartheta} \xdef\a{\alpha} \xdef\vf{\varphi} \xdef\Tagged#1{(\text{#1})} \xdef\tagged*#1{\text{#1}} \xdef\tagEqHere#1#2{\href{#2\#eq-#1}{(\text{#1})}} \xdef\tagDeHere#1#2{\href{#2\#de-#1}{\text{#1}}} \xdef\tagEq#1{\href{\#eq-#1}{(\text{#1})}} \xdef\tagDe#1{\href{\#de-#1}{\text{#1}}} \xdef\T#1{\htmlId{eq-#1}{#1}} \xdef\D#1{\htmlId{de-#1}{\vv{#1}}} \xdef\conv#1{\mathrm{conv}\, #1} \xdef\cone#1{\mathrm{cone}\, #1} \xdef\aff#1{\mathrm{aff}\, #1} \xdef\lin#1{\mathrm{Lin}\, #1} \xdef\span#1{\mathrm{span}\, #1} \xdef\O{\mathcal O} \xdef\ri#1{\mathrm{ri}\, #1} \xdef\rd#1{\mathrm{r}\partial\, #1} \xdef\interior#1{\mathrm{int}\, #1} \xdef\proj{\Pi} \xdef\epi#1{\mathrm{epi}\, #1} \xdef\grad#1{\mathrm{grad}\, #1} \xdef\gradT#1{\mathrm{grad}^T #1} \xdef\gradx#1{\mathrm{grad}_x #1} \xdef\hess#1{\nabla^2\, #1} \xdef\hessx#1{\nabla^2_x #1} \xdef\jacobx#1{D_x #1} \xdef\jacob#1{D #1} \xdef\subdif#1{\partial #1} \xdef\co#1{\mathrm{co}\, #1} \xdef\iter#1{^{[#1]}} \xdef\str{^*} \xdef\spv{\mcal V} \xdef\civ{\mcal U} \xdef\other#1{\hat{#1}} $$

Přehled her

Bimaticové hry 2x2

Mějme $$ A = \mtr{a & b \ c & d}, \quad B = \mtr{e & f \ g & h} $$

V případě dominování, např. $a > b \;\and\; c > d$ , je to jednoduché... Tedy předpokládejme, že žádný řádek nedominuje pro 1. hráče a žádný sloupec pro 2. hráče.

A tedy $$ u(p,q) = \mtr{p & 1-p} A \mtr{q \ 1-q}, \ v(p,q) = \mtr{p & 1-p} B \mtr{q \ 1-q} $$

Rovnováhy

Hráč 2 chce zabránit volit tomu prvnímu a tedy indiferenční rovnice je tvaru $$ u(0, q) = u(1,q) \ \mtr{c & d} \mtr{q \ 1-q} = \mtr{a & b} \mtr{q \ 1-q} \ (c - d)q + d = (a - b)q + b \ (a-b-c+d)q = d-b $$ $$ q = {d-b \over a - b - c + d} $$ a opačně $$ v(p,0) = v(p,1) \ \mtr{p & 1 - p} \mtr{f \ h} = \mtr{p & 1 - p} \mtr{e \ g} \ \mtr{p & 1 - p} \mtr{f-e \ h-g} = 0 \ p(f-e-h+g) - h-g = 0 $$ $$ p = {g-h \over f-e-g+h} $$

Pak tedy rovnovážná strategie ve smíšených strategiích je tvaru $(p,q)$

Dolní hodnota

Počítejme $h_1^-$ a tedy bychom chtěli zjistit, jak máme volit $p$, aby nám bylo jedno, jak hraje 2. hráč $$ u(p, 0) = u(p,1) \ \mtr{p & 1 - p} \mtr{b \ d} = \mtr{p & 1 - p} \mtr{a \ c} \ \vdots $$ $$ p = {d-c \over a-b-c+d} $$

Příklady her 2x2

Mějme $$ A = \mtr{1 & -2 \ -3 & 4} \to \mtr{4 &1 \ 0 & 7} \to \mtr{4/7 & 1/7 \ 0 & 1} $$

Normalizace hry: První posunume hru do kladných čísel, pak ji "zmenšíme" tak, že největší výhra 1 Tj.

1. $\min A = 0$
2. $\max A = 1$

Pozor, pořád jsou to ekvivalentní hry!!

Přehled základních her 2x2

Prozkoumejme čtveřici $(0, 1, 2, 3)$

1. mince $$ A = \mtr{1 & 0 \ 0 & 1}, \quad B = \mtr{0 & 1 \ 1 & 0} $$ tato hra není symetrická, ale je "spravedlivá" (kdyby si vyměnili role, tak jim to nepomůže). Zřejmě ani jeden z hráčů nemá dominovanou strategii. Počítejme rovnováhu $$ q = {1-0 \ 1 - 0 - 0 + 1}= \frac 1 2 = \dots = p $$ a rovnováha je $(p,q) = (\frac 1 2, \frac 1 2)$. Přičemž dolní hodnota $$ q = \frac {1-0} {1 -0 - 0 + 1} = \frac 1 2 $$ a proto $h_1^- = \frac 1 2$
2. na kočku a myš
   Kočka má na výběr z vytápěné/nevytápěné místnosti (světice/komora) $$ A = \mtr{3 & 1 \ 0 & 2}, \quad B = \mtr{0 & 3 \ 2 & 1} $$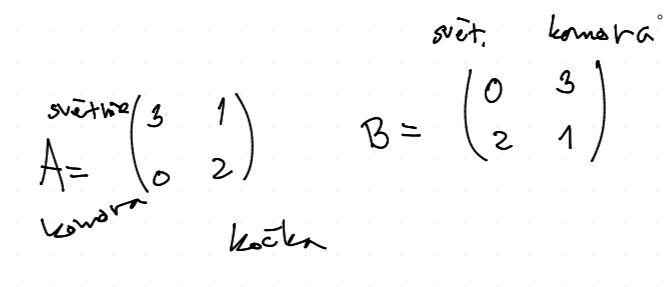
   A tedy máme situace $$ (3, 0) \quad (1,3) \succ (0,2) \quad (1,2) $$ Tato hra není ani antagonistická, ani s nulovým součtem. Evidentně existuje rovnováha pouze v smíšených situacích
3. líný rodič
   Rodiče chtějí, aby potomek přežil, ale chceme se flákat a nechat to na tom druhém. Je to jistě symetrická hra $$ \nmtr{\text{stará se} \ \text{nestará se}} \mtr{2 & 1 \ 3 & 0}, \qquad ()^T = \mtr{2 & 3 \ 1 & 0} $$ a potom máme situace $$ (0,0) \prec (2,2), \underbrace{(1,3), (3,1)}_ {\textbf{rovnováhy} \text{ v čistých}} $$ Rozhodně nejde o hru, která aby antagonistická nebo s nulovým součtem.
   Ve smíšených strategiích $$ q = {d-b \over a - b - c + d} = \frac {-1} {-2} = \frac 1 2 = \text{symetrie} = p $$ a tedy $u(\frac 1 2, \frac 1 2) = \mtr{\frac 1 2 & \frac 1 2} \mtr{\frac 1 2 \ \frac 1 2} = \frac 3 2$. Tedy je lepší, aby se oba rodiče starali, než kdyby to nechali na náhodu
4. na kuře
   Jedeme proti sobě autem a pokud uhnu dřív, než soupeř, tak jsem prohrál a jsem zbabělec $$ \nmtr{\text{uhnu} \ \text{zůstanu}} \mtr{0 & -1 \ 1 & -10} $$ Po normalizaci dostaneme hru tvaru líný rodič.
5. lov na jelena
   Máme 2 lovce, kteří se nemohou domluvit. Pokud loví dohromady, tak mají šanci ulovit jelena, ale jeden sám ho neuloví. Navíc můžeme ulovit max 2 zajíce, kteří jsou v lese. $$ \nmtr{\text{jdu na jelena} \ \text{jdu na zajíce}} \mtr{3 & 0 \ 2 & 1} \; \and \; \mtr{3 & 2 \ 0 & 1} $$ Potom situace rovnováhy jsou $(1,1), (3,3)$, přičemž z ní "jednostraně" nemůžeme uhnout. Navíc $(3,3)$ je dominující strategií (je optimální). Jediná opatrná strategie je zde jít si pro zajíce.

   Ilustruje, že příroda si může vybrat rovnováhu, která není nejlepší - přechod na nejlepší rovnováhu by vyžadoval domluvu.

6. vězňovo dilema
   Máme 2 vězně, kde každý má na výběr buď mlčet (spolupracovat s spolupachatelem) nebo to zkusím hodit na spolupachatele (zradit). Jistě je to navíc symetrická hra $$ \nmtr{\text{spolupracovat} \ \text{zradit}} \mtr{-1 & -3 \ 0 & -2} \to \mtr{2 & 0 \ 3 & 1} $$ Po normalizaci si snažíme maximalizovat roky na svobodě (snažíme si ušetřit trest). Jistě navíc $$ \text{spolupracovat} \prec \text{zradit} $$ Přičemž $(2,2)$ je jediná rovnovážná situace i ve smíšených strategiích.

   V případě opakované hry se rozhodujeme v závislosti na předchozích rozhodnutích. Můžeme řešit pomocí stavového automatu:
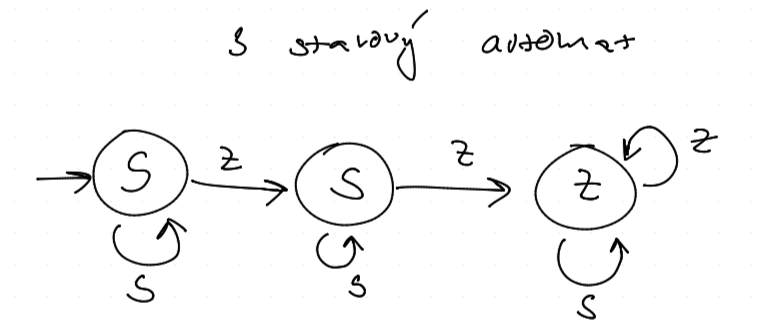
   a celkem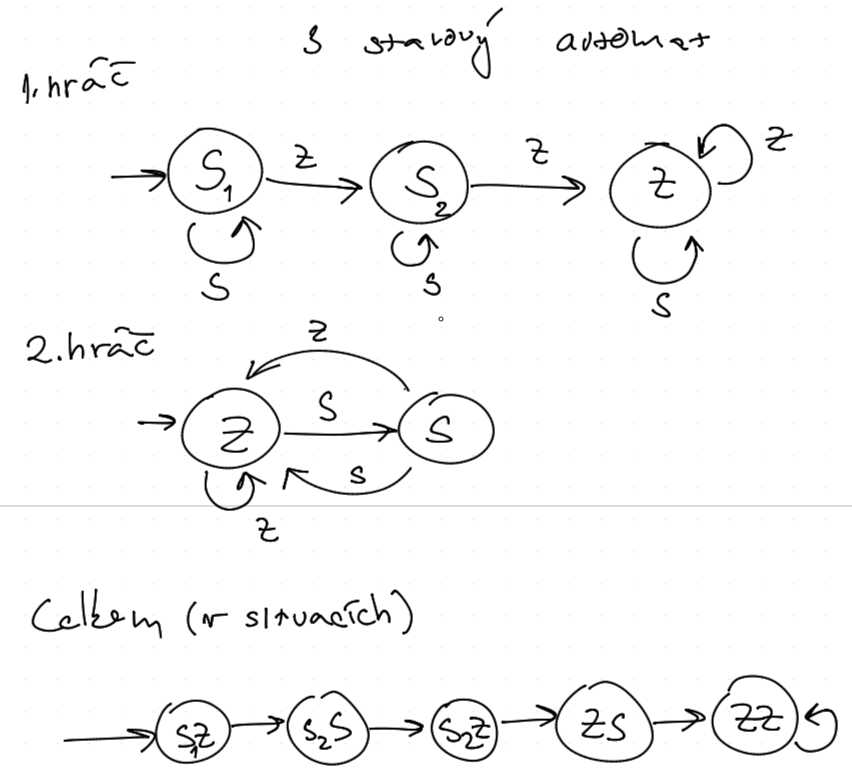
   Přičemž automaty jsou "strategie s omezenou pamětí"