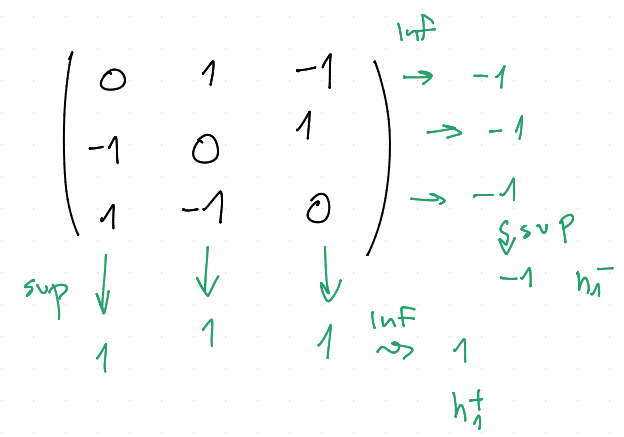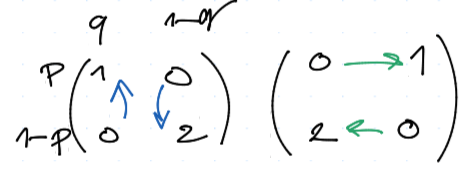2. přednáška
$$ \xdef\scal#1#2{\langle #1, #2 \rangle} \xdef\norm#1{\left\lVert #1 \right\rVert} \xdef\dist{\rho} \xdef\and{\&}\xdef\AND{\quad \and \quad}\xdef\brackets#1{\left\{ #1 \right\}} \xdef\parc#1#2{\frac {\partial #1}{\partial #2}} \xdef\mtr#1{\begin{pmatrix}#1\end{pmatrix}} \xdef\bm#1{\boldsymbol{#1}} \xdef\mcal#1{\mathcal{#1}} \xdef\vv#1{\mathbf{#1}}\xdef\vvp#1{\pmb{#1}} \xdef\ve{\varepsilon} \xdef\l{\lambda} \xdef\th{\vartheta} \xdef\a{\alpha} \xdef\vf{\varphi} \xdef\Tagged#1{(\text{#1})} \xdef\tagged*#1{\text{#1}} \xdef\tagEqHere#1#2{\href{#2\#eq-#1}{(\text{#1})}} \xdef\tagDeHere#1#2{\href{#2\#de-#1}{\text{#1}}} \xdef\tagEq#1{\href{\#eq-#1}{(\text{#1})}} \xdef\tagDe#1{\href{\#de-#1}{\text{#1}}} \xdef\T#1{\htmlId{eq-#1}{#1}} \xdef\D#1{\htmlId{de-#1}{\vv{#1}}} \xdef\conv#1{\mathrm{conv}\, #1} \xdef\cone#1{\mathrm{cone}\, #1} \xdef\aff#1{\mathrm{aff}\, #1} \xdef\lin#1{\mathrm{Lin}\, #1} \xdef\span#1{\mathrm{span}\, #1} \xdef\O{\mathcal O} \xdef\ri#1{\mathrm{ri}\, #1} \xdef\rd#1{\mathrm{r}\partial\, #1} \xdef\interior#1{\mathrm{int}\, #1} \xdef\proj{\Pi} \xdef\epi#1{\mathrm{epi}\, #1} \xdef\grad#1{\mathrm{grad}\, #1} \xdef\gradT#1{\mathrm{grad}^T #1} \xdef\gradx#1{\mathrm{grad}_x #1} \xdef\hess#1{\nabla^2\, #1} \xdef\hessx#1{\nabla^2_x #1} \xdef\jacobx#1{D_x #1} \xdef\jacob#1{D #1} \xdef\subdif#1{\partial #1} \xdef\co#1{\mathrm{co}\, #1} \xdef\iter#1{^{[#1]}} \xdef\str{^*} \xdef\spv{\mcal V} \xdef\civ{\mcal U} \xdef\other#1{\hat{#1}} $$
Definice $\D{KON}$ (Konečná hra)
Mějme množinu hráčů $N = \set{1, 2, \dots, n}$. Pak hra $G = (M, X_i, u_i)$ je konečná, pokud jsou $X_i$ konečné.
Na konečných hrách můžeme zavést tzv. pravděpodobností rozšíření
Definice $\D{SYM}$ (Symetrická hra)
Hra $G$ 2 hráčů je symetrická právě tehdy, když $u(x,y) = v(y, x)$. V případě bimaticových her to je ekvivalentní s podmínkou $$ U^T = V $$
Příklad (kámen, nůžky, papír)
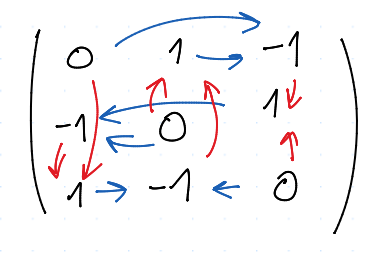
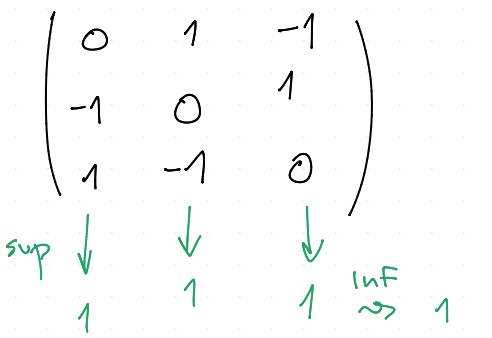
Mějme 2 hráče, tj. $N = \set {1, 2}$ a $X = Y = \set{ \mcal K, \mcal N, \mcal P }$. Jelikož je to bimaticová hra, tak výhra je dána jako $$ U = \mtr{ 0 & 1 & -1 \ -1 & 0 & 1 \ 1 & -1 & 0 \ } $$
Sloupce a řádky jsou indexovány $\mcal K, \mcal N, \mcal P$
Podívejme se na Nashovu rovnováhu, tj. $$ u(x,y) \geq u(\bar x, y) \quad \text{pro libovolné } \bar x \ v(x,y) \geq v(x, \bar y) \quad \text{pro libovolné } \bar y \ $$
Aneb si odbočením do jiného řádku si nepomůžeme
Aby nastala rovnováha, tak musí $u(x,y) = 1$, tj. $v(x,y) = 1$. Ale druhý hráč by mohl hrát $\bar y$ tak, že $v(x, \bar y) = 1$.
Zde si všimněme, že pokud půjdeme podle šipek, tak nikdy neskončíme
Dominance by zde znamenalo, že by jeden řádek, byl větší než nějaký jiný - aneb 2 řádky by musely být porovnatelné (jakožto vektory)
Dolní hodnota $$ h_ 1^- = \sup_ x \inf_ y u(x,y) $$
a horní hodnota
Definice $\D{PRA}$ (Pravděpodobnostní rozšíření)
Mějme konečnou hru $G = (M, X_i, u_i)$. Pak definujeme pravděpodobnostní rozšíření $$ G\str = (N, X_i\str, u_i\str), $$ kde $X_i\str = \set{a_i^1 x_i^1 + a_i^2 x_i^2 + \dots + a_i^{m_i} x_i^{m_i} \mid x_i^j \in X_i \; \land \; a_ i^1 + \dots + a_i^{m_ i} = 1 \; \land \; a_i^j > 0}$ je množina konvexních kombinací strategií a pro výhry platí $$ u_i\str(\vv x\str) = \sum_{(x_1^{j_1}, \dots, x_n^{j_n}) \in \prod X_i} a_1^{j_1} a_2^{j_2} \cdot \ldots \cdot a^{j_n}_n \cdot u_i(x^{j_1}_1, \dots, x^{j_1}_n) $$
Pokračování příkladu
Počítejme pravděpodobnostní rozšíření, tj. $$ u\str((p_1, p_2), (q_1, q_2)) = p_1 q_1 \overbrace{u(\mcal K, \mcal K)}^0 + p_1 q_2 \overbrace{u(\mcal K, \mcal N)}^1 + p_1 (1 - q_1 - q_2) u(\mcal K, \mcal P) + \dots $$ kde
- $p_1$ je pravděpodobnost zahrání $\mcal K$ prvním hráčem
- $p_2$ je pravděpodobnost zahrání $\mcal N$ prvním hráčem
- $q_1$ je pravděpodobnost zahrání $\mcal K$ druhým hráčem
- $q_2$ je pravděpodobnost zahrání $\mcal N$ druhým hráčem
- $1 - p_1 - p_2$ je pravděpodobnost zahrání $\mcal P$ prvním hráčem
To ale můžeme napsat jako $$ u\str((p_1, p_2), (q_1, q_2)) = \mtr{p_1 & p_2 & (1 - p_1 - p_2)} U \mtr{q_1 \ q_2 \ 1 - q_1 - q_2} $$
Potom pro $$ \mtr {1/3 & 1/3 & 1/3} U = \mtr{0 & 0 & 0} \ \mtr{0 & 0 & 0} \mtr{q_1 \ q_2 \ 1 - q_1 - q_2} = 0 $$ Tedy strategie $(1/3, 1/3, 1/3)$ a $(1/3, 1/3, 1/3)$ tvoří rovnovážnou situaci a navíc $$ h_1^{* -} = h_1^{* +} = 0 $$
Prvky $x_1\str \in X_i\str$ nazýváme smíšené strategie a původní strategie do tohoto nového prostoru vnoříme volbou pravděpodobnostího rozdělení $(0, \dots, 0, 1, 0, \dots, 0)$. V tomto smyslu takovým strategiím říkáme čisté strategie
Věta $\D{NASH}$ (Nashova)
Pravděpodobnostní rozšíření každé konečné hry má rovnovážnou situaci.
Důkaz
Mějme rovnováhu $\vv x$, tj. $$ u_i\str(\vv x) \geq u_i\str(x_i\str, x_{\other i}\str) $$ Dále označme $B_i(x_{\other i}\str)$ nejlepší odpovědi na volbu protihráčů $x_{\other i}\str$. Tedy $\vv x$ je rovnováha právě tehdy, když $$ \forall i \in N: \quad x_i\str \in B_i(x_{\other i}\str) $$ Tedy $B_i : \prod_{j \neq i} X_j \str \to \mcal P (X_i\str)$ a pokud dáme $B_i$ dohromady jako $$ B = (B_ i)_ {i \in N}, \qquad B : \prod_ {i \in N} X_i\str \to \prod_{i \in N} \mcal P (X_i\str) $$
Pod $\mcal P$ zde myslíme "power set" (potenční množina) - pro jednu situaci může být více nejlepších strategií (odpovědí)
$B$ je tedy (množinová) funkce na prostoru situací. Podle Kakutanyho věty o pevném bodě existuje $x\str \in B(x\str)$, což je rovnovážná situace. $\blacksquare$
Mějme $$ u(\vv x) = (x) U (y) $$
V rovnovážně situaci nám budou vycházet stěny polyedru
Příklad - využití pro (bi)maticové hry
Mějme $$ U = \mtr{1 & 0 \ 0 & 2}, V = \mtr{0 & 1 \ 2 & 0} $$
Tedy celkem $$ u(p,q) = pq + 2(1-p)(1-q) \ v(p,q) = p(1 - q) + 2(1 - p)q $$
Rovnováha je tak, že druhý hráč nemá kam pohnout (je mu to jedno)
Indiferenční rovnice - chceme zařídit, aby $u$ nezáviselo na $p$ a $v$ na $q$
V našem případě $$ u(p,q) = p(\underbrace{q - 2 + 2q}_0) + 2(1-q) \implies 3q - 2 = 0 \implies q = {2 \over 3} \ v(p,q) = q(\underbrace{-p + 2 - 2p}_0) + p \implies 3p - 2 = 0 \implies p = \frac 2 3 $$
Tedy pravděpodobnostní rozdělení $((2/3, 1/3), (2/3, 1/3))$ tvoří rovnovážnou situaci a $$ u(\vv x\str) = \frac 2 3, \qquad v(\vv x\str) = \frac 2 3 $$
Věta $\D{ANT}$
U antagonistických her platí, že strategie je optimální právě tehdy, když je opatrná. Řekneme, že strategie $x_i$ je opatrná, pokud zaručuje $h_i^-$.
Strategii nazveme optimální, pokud tato strategie realizuje nějakou rovnovážnou situaci
Pokud počítáme $h_1^-$, tak "zjišťujeme, co mi může soupeř provést", tj. $$ \begin{align*} u(p,q) &= q(p - 2 + 2q) + 2(1-p) \ &= q(\underbrace{3p - 2}_0) + 2(1-p) \ &= \frac 2 3 \end{align*} $$
Při zvýšení $p$ dá soupeř $q = 0$ a já si pohorším, naopak s menším $p$ dává soupeř $q = 1$
Tedy $h_1^- = \frac 2 3$ a tato strategie je opatrná.
Pravděpodobnostní rozšíření na nekonečných prostorech se konstruuje přes míry a Riemann-Stiltjesův integrál