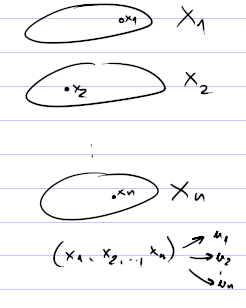1. přednáška
$$ \xdef\scal#1#2{\langle #1, #2 \rangle} \xdef\norm#1{\left\lVert #1 \right\rVert} \xdef\dist{\rho} \xdef\and{\&}\xdef\AND{\quad \and \quad}\xdef\brackets#1{\left\{ #1 \right\}} \xdef\parc#1#2{\frac {\partial #1}{\partial #2}} \xdef\mtr#1{\begin{pmatrix}#1\end{pmatrix}} \xdef\bm#1{\boldsymbol{#1}} \xdef\mcal#1{\mathcal{#1}} \xdef\vv#1{\mathbf{#1}}\xdef\vvp#1{\pmb{#1}} \xdef\ve{\varepsilon} \xdef\l{\lambda} \xdef\th{\vartheta} \xdef\a{\alpha} \xdef\vf{\varphi} \xdef\Tagged#1{(\text{#1})} \xdef\tagged*#1{\text{#1}} \xdef\tagEqHere#1#2{\href{#2\#eq-#1}{(\text{#1})}} \xdef\tagDeHere#1#2{\href{#2\#de-#1}{\text{#1}}} \xdef\tagEq#1{\href{\#eq-#1}{(\text{#1})}} \xdef\tagDe#1{\href{\#de-#1}{\text{#1}}} \xdef\T#1{\htmlId{eq-#1}{#1}} \xdef\D#1{\htmlId{de-#1}{\vv{#1}}} \xdef\conv#1{\mathrm{conv}\, #1} \xdef\cone#1{\mathrm{cone}\, #1} \xdef\aff#1{\mathrm{aff}\, #1} \xdef\lin#1{\mathrm{Lin}\, #1} \xdef\span#1{\mathrm{span}\, #1} \xdef\O{\mathcal O} \xdef\ri#1{\mathrm{ri}\, #1} \xdef\rd#1{\mathrm{r}\partial\, #1} \xdef\interior#1{\mathrm{int}\, #1} \xdef\proj{\Pi} \xdef\epi#1{\mathrm{epi}\, #1} \xdef\grad#1{\mathrm{grad}\, #1} \xdef\gradT#1{\mathrm{grad}^T #1} \xdef\gradx#1{\mathrm{grad}_x #1} \xdef\hess#1{\nabla^2\, #1} \xdef\hessx#1{\nabla^2_x #1} \xdef\jacobx#1{D_x #1} \xdef\jacob#1{D #1} \xdef\subdif#1{\partial #1} \xdef\co#1{\mathrm{co}\, #1} \xdef\iter#1{^{[#1]}} \xdef\str{^*} \xdef\spv{\mcal V} \xdef\civ{\mcal U} \xdef\other#1{\hat{#1}} $$
V jakémsi smyslu zobecnění optimalizace, kdy máme více hráčů
Úvodní příklad (hra ultimátum)
Mějme $I = [0, 1]$ a 1. hráč si vybere $x \in I$ a 2. hráč říká ano/ne na vybrané $x$.
Hry v normální formě
Definice $\D{HNF}$ (Hra v normální formě)
Mějme $n \in \N$ a $N = \set{1, 2, \dots, n}$ je množina hráčů. A zaveďme
- $X_i$ - množina strategií $i$-tého hráče
- $u_i$ - výherní funkce $i$-tého hráče ($\prod$ je zde kartézský součin)
$$u_i : \prod_{i \in N} X_i \to \R$$
Řekneme, že strategie $x_i$ dominuje $y_i$, značíme $ X_i \succ Y_i$. Navíc značíme $x_{\other i} = (x_1, \dots, x_{i - 1}, x_{i+1}, \dots, x_n)$ a pak $$ u_i(x_i, x_{\other i}) \geq u_i(y_i, x_{\other i}) \quad \forall x_{\other i} \quad \and \quad \exists x_{\other i} \quad u_i(x_i, x_{\other i}) > u_i(y_i, x_{\other i}) $$
Strategie $x$ je nedominovaná, jestliže neexistuje $y \succ x$.
Pokračování úvodního příkladů
$$ X_1 = I \ X_2 = \set{0,1}^I, $$ kde $\set{0,1}^I$ je množina zobrazení z $I$ do $\set{0,1}$. Pak výherní funkce jsou $$ u_1(x, f) = \begin{cases} x, & \text{ pro } f(x) = 1 \ 0, & \text{ pro } f(x) = 0 \end{cases} $$ $$ u_2(x, f) = \begin{cases} 1 - x, & \text{ pro } f(x) = 1 \ 0, & \text{ pro } f(x) = 0 \end{cases} $$
Pro 1. hráče jistě $0 \prec x$ pro $x \neq 0$, protože $$ u_i(0, f_{\other i}) = 0 $$ ale $$ u_i(x, f_{\other i}) = \begin{cases} x, & \text{ pro } f(x) = 1 \ 0, & \text{ pro } f(x) = 0 \end{cases} \geq 0 $$ Pro 2. hráče $f \prec g$ nastane právě tehdy, když v $g$ souhlasíme ve více případech, tj. $$ \forall x : f(x) = 1 \implies g(x) = 1 \quad \and \quad \exists x : f(x) = 0 \land g(x) = 1 $$ Jinak zapsáno $f < g$.
Nyní předpokládejme $x \prec y, \; x,y > 0, x \neq y$, tj. hledáme $$ f : u_1(x, f_{\hat i}) > u_1(y, f_{\hat i}) $$ a pak stačí libovolná $f$, že $f(x) = 1, f(y) = 0$, z čehož dostaneme $1 > 0$.
Z pohledu řešení hry je rozumné neuvažovat libovolné dominované strategie. Tímto jsme ji ale vytrhli z kontextu. Tedy zde by si odmítnutím "budoval prestiž" na další hry. Zde by totiž 1. hráč si mohl vzít (skoro) celý interval (rohlík) a podle nedominované strategie by to 2. hráč přijal.
Definice $\D{SIT}$ (Situace)
Sitaucí nazveme $n$-tici $(x_1, \dots, x_n) \in \prod_{i \in N} X_i$.
Řekneme, že situace $\vv x = (x_1, \dots, x_n)$ dominuje podle Pareta sitauci $\vv y = (y_1, \dots, y_n)$, pokud $$ \forall i \in N : u_i (\vv x) \geq u_i (\vv y) \AND \exists i \in N : u_i (\vv x) > u_i (\vv y) $$
Pokračování úvodního příkladů
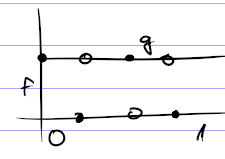
Například $x = \frac 2 3$ a $f(x) = \begin{cases} 1, & x \leq \frac 1 2 \ 0, & \text{jinak}\end{cases}$.
V tomto případě pro $(x, f)$ mají $u_1(x, f) = u_2(x,f) = 0$.
Naopak $y = \frac 1 2$ a $g(x) = \begin{cases} 1, & x \leq \frac 2 3 \ 0, & \text{jinak}\end{cases}$.
V tomto případě pro $(x, f)$ mají $$ u_1(y, g) = u_2(y, g) = \frac 1 2 $$
A tedy $(x,f) \prec (y,g)$ .
Pokud se dohodnou v obou situacích, pak o jejich dominování nemůžeme mluvit - jeden dostane méně, druhý více.
Definice $\D{ZAR}$ (Zaručování)
Hráč $i$ si zaručuje $x$, pokud $$ \exists x_ i : \forall x_ {\other i} : u_ i(x_ i, x_ {\other i}) \geq x $$ Dolní hodnotou hry pro $i$-tého hráče je $$ h^-_ i = \sup _ {x_ i} \inf_ {x_ {\other i}} = u_ i (x_i, x_{\other i}) $$
Horní hodnotou hry pro $i$-tého hráče je $$ h^+_ i = \inf_ {x_ i} \sup_ {x_ {\other i}} = u_ i (x_i, x_{\other i}) $$
U dolní hodnoty "škodící" hráči dopředu ví, co zahraji (první děláme volíme v infimu, potom až v supremu)
Pro úvodní příklad je $$ h_1^ - = h_2^ - = 0 $$ a $$ h_1^ + = h_2^ + = 0 $$
Definice $\D{ROV}$ (Rovnovážná situace)
Řekneme, že $\vv x$ je rovnovážná situace (Nashova rovnováha), pokud $$ \forall i \in N : \forall y_i \in X_i : u_i(x_i, x_{\other i}) \geq u_i (y_i, x_{\other i}) $$
Pro každého hráče samostatně je dobré hrát takto
Mějme $(x, f)$ pro $x > 0$, pak pro $f(y) = \begin{cases}1, & y \leq x \ 0, & y > x\end{cases}$. Změňme $x \to y$, pak pokud
- $y < x$, pak $u_1(x,f) = x$ a $u_1(y,f) = y < x$
- $y > x$, pak $u_1(x,f) = x$ a $u_1(y,f) = 0 < x$
Nyní změňme $f \to g$, pak pro $g(x) = 1$ je $u_2(x,f) = x = u_2(x,g)$. Naopak pro $g(x) = 0$ je $u_2(x,g) = 0 \leq u_2(x,f)$.
Hra 2 hráčů
Zde $n = 2$ a značme
- $x_1$ jako $x$, $X_1$ jako $X$
- $x_2$ jako $y$, $X_2$ jako $Y$
- $u_1$ jako $u$
- $u_2$ jako $v$
Antagonistická hra je taková, že pro situace $(x,y)$ a $(\bar x, \bar y)$, tak pokud $$ u(x,y) \geq u(\bar x, \bar y) \iff v(x,y) \leq v(\bar x, \bar y) $$
Paretovská dominance vylučuje antagonistickou hru
Hra s konstatním součtem nazýváme hru, kde $$ u(x,y) + v(x,y) = c $$ a speciální případ jsou hry s nulovým součtem, kde $$ u(x,y) + v(x,y) = 0 $$
Šachy jsou hra s konstantím součtem (výhra - 1, remíza - 0.5). Naopak fotbal není (výhra - 3, remíza - 1), ale je antagonistická.
U koopertivních her mají hráči nějakým způsobem možnost dosahovat paretovské dominance
Definice $\D{MAT}$ (Maticová hra)
HraMějme hru 2 hráčů, kde množiny $X,Y$ jsou konečné. Pišme
$$
X = \set{x_1, \dots, x_k} \AND Y = \set{y_1, \dots, y_l}
$$
a pak situace uspořádáme do matice $X \times Y$ následovně
Matice $A,B$ jsou pak výherní matice 1. a 2. hráče a $u(x_i, y_j) = A_{i,j}$.