Skip to main content

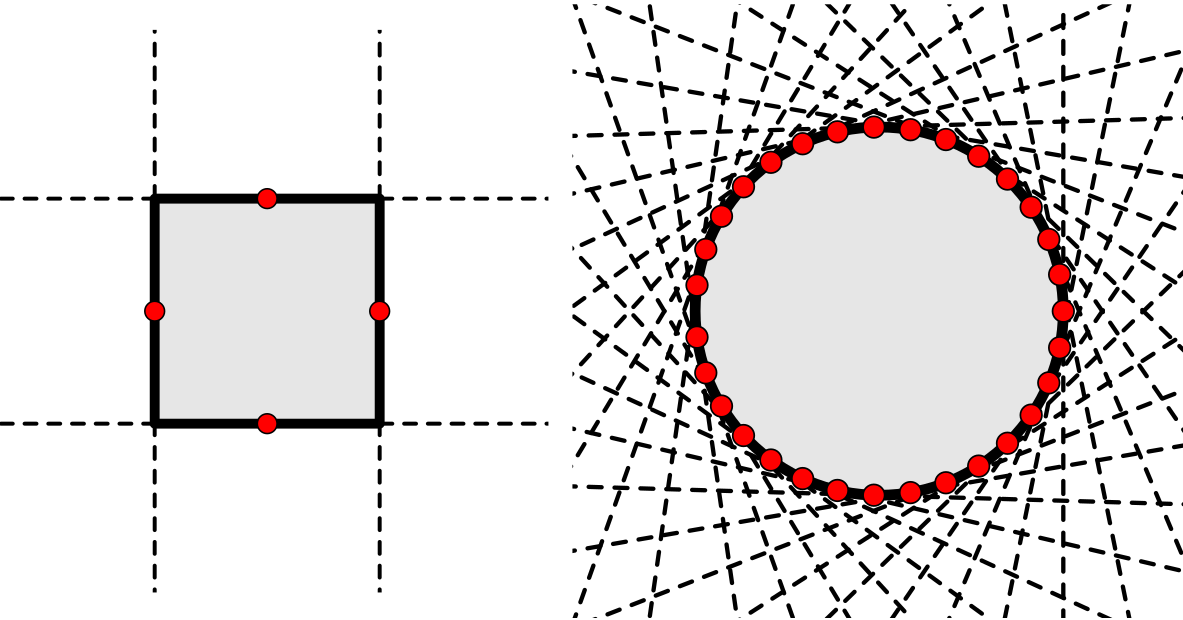
Oddělování konvexních množin

\xdef\scal#1#2{\langle #1, #2 \rangle} \xdef\norm#1{\left\lVert #1 \right\rVert} \xdef\dist{\rho} \xdef\and{\&}\xdef\brackets#1{\left\{ #1 \right\}} \xdef\parc#1#2{\frac {\partial #1}{\partial #2}} \xdef\mtr#1{\begin{pmatrix}#1\end{pmatrix}} \xdef\bm#1{\boldsymbol{#1}} \xdef\vv#1{\mathbf{#1}}\xdef\vvp#1{\pmb{#1}} \xdef\ve{\varepsilon} \xdef\l{\lambda} \xdef\a{\alpha} \xdef\tagged#1{(\text{#1})} \xdef\conv#1{\mathrm{conv}\, #1} \xdef\cone#1{\mathrm{cone}\, #1} \xdef\aff#1{\mathrm{aff}\, #1} \xdef\lin#1{\mathrm{Lin}\, #1} \xdef\span#1{\mathrm{span}\, #1} \xdef\O{\mathcal O} \xdef\ri#1{\mathrm{ri}\, #1} \xdef\rd#1{\mathrm{r}\partial\, #1} \xdef\interior#1{\mathrm{int}\, #1} \xdef\proj{\Pi}

Oddělitelnost množin

Definice 2.3.1 (Oddělitelnost množin)

Neprázdné množiny X1,X2X_1, X_2 se nazývají

  • oddělitelné, jestliže existuje p∈Rn∖{0}p \in \R^n \setminus \brackets{\vv 0} takové, že
    ⟨p,x1⟩≥⟨p,x2⟩\scal p {x_1} \geq \scal p {x_2} pro každé x1∈X1,x2∈X2x_1 \in X_1, x_2 \in X_2.
  • vlastně oddělitelné, jestliže jsou oddělitelné a zároveň existují body x1∗∈X1,x2∗∈X2x_1^* \in X_1, x_2^* \in X_2 takové, že
    ⟨p,x1∗⟩>⟨p,x2∗⟩\scal p {x_1^* } > \scal p {x_2^* }
  • silně oddělitelné, jestliže existuje p∈Rn∖{0}p \in \R^n \setminus \brackets{\vv 0} takové, že
    inf⁡x1∈x1⟨p,x1⟩>sup⁡x2∈X2⟨p,x2⟩,\inf_{x_1 \in x_1} \scal p {x_1} > \sup_{x_2 \in X_2} \scal p {x_2}, je-li navíc β∈[sup⁡x2∈X2⟨p,x2⟩,inf⁡x1∈X1⟨p,x1⟩]\beta \in [\sup_{x_2 \in X_2} \scal p {x_2}, \inf_{x_1 \in X_1} \scal p {x_1}], nadrovina Hp,β:={x∈Rn∣⟨p,x⟩=β}H_{p,\beta} := \brackets{x \in \R^n \mid \scal p x = \beta} se nazývá oddělující narovinou množin X1X_1 a X2X_2.

Ve vyjádření {x∈Rn∣⟨p,x⟩=β}\brackets{x \in \R^n \mid \scal p x = \beta} značí pp normálový vektor nadroviny a β\beta její posunutí

Definice 2.3.2 (Projekce bodu)

Nechť X⊆RnX \subseteq \R^n je neprázdná množina a x∈Rnx \in \R^n. Bod x∗∈Xx^* \in X nazveme projekcí bodu xx na množinu XX a označíme ΠX(x)\proj_X (x), jestliže ∥ΠX(x)−x∥≤∥y−x∥ \norm{\proj_X (x) - x} \leq \norm{y - x} pro každé y∈Xy \in X.

Věta 2.3.4

Neprázdné konvexní množiny X1,X2∈RnX_1,X_2 \in \R^n jsou silně oddělitelné právě tehdy, když mají nenulovou vzdálenost, tj. ρ(X1,X2):=inf⁡x1∈X1,x2∈X2∥x1−x2∥>0, \dist (X_1, X_2) := \inf_{x_1 \in X_1, x_2 \in X_2} \norm{x_1 - x_2} > 0, což je ekvivalentní s podmínkou 0∉X1−X2‾0 \notin \overline{X_1 - X_2}.

Pod kompaktní množinou myslíme množinu, která je ohraničená (má konečný průměr) a uzavřená (obsahuje svou hranici).

Pokud jsou množiny X1,X2⊆RnX_1, X_2 \subseteq \R^n neprázdné, konvexní a disjunktní a navíc BÚNO je X1X_1 ohraničená a X2X_2 kompaktní, tak jsou množiny silně oddělitelné.
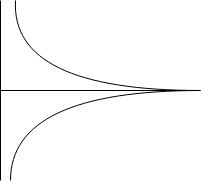
Požadavek kompaktnosti množiny X2X_2 vynechat nelze, viz protipříklad dvou hyperbol (obrázek je pouze ilustrativní)

Věta 2.3.5a (Geometrický popis konvexních množin)

Libovolná uzavřená konvexní množina X⊆RnX \subseteq \R^n je řešením (nekonečné) soustavy neostrých lineárních rovnic.

Geometricky: každá uzavřená konvexní množina X⫋RnX \subsetneqq \R^n je průnikem uzavřených poloprostorů, konkrétně všech uzavřených poloprostorů obsahujících XX

Opěrné nadroviny

Definice 2.3.6 (Opěrná nadrovina)

Nechť X⊆RnX \subseteq \R^n je neprázdná množina a nechť a∈∂X:=X‾∖int Xa \in \partial X := \overline X \setminus \interior X. Nadrovina Hp,βH_{p, \beta} se nazývá

  • opěrnou nadrovinou množiny XX v bodě aa, jestliže
    ⟨p,x⟩≥β=⟨p,a⟩\scal p x \geq \beta = \scal p a pro každé x∈Xx \in X
  • vlastní opěrnou nadrovinou množiny XX, jestliže je opěrnou nadrovinou množiny XX a zároveň existuje x∗∈Xx^* \in X takové, že
    ⟨p,x∗⟩>β\scal p {x^* } > \beta

Jinak řečeno množina musí ležet pouze v jednom z poloprostorů určených opěrnou nadrovinou.

Věta 2.3.7 (Existenci opěrné nadroviny)

Nechť X⊆RnX \subseteq \R^n je neprázdná konvexní množina a nechť a∈r∂ X⊆∂Xa \in \rd X \subseteq \partial X. Pak v bodě aa existuje vlastní opěrná nadrovina množiny XX.

Pro relativní vnitřek ri X\ri X množiny XX a její vnitřek platí int X⊆ri X\interior X \subseteq \ri X a tedy jistě
X‾∖ri X=r∂ X⊆∂X=X‾∖int X\overline X \setminus \ri X = \rd X \subseteq \partial X = \overline X \setminus \interior X

Podmínky oddělitelnosti

Věta 2.3.7a (Oddělitelnost množin)

Nechť X1,X2⊆RnX_1, X_2 \subseteq \R^n jsou neprázdné, konvexní a disjunktní množiny. Pak pro tyto množiny existuje oddělující nadrovina.

Věta 2.3.8

Neprázdné konvexní množiny X1,X2⊆RnX_1, X_2 \subseteq \R^n jsou vlastně oddělitelné právě tehdy, když ri X1∩ri X2=∅\ri X_1 \cap \ri X_2 = \emptyset.

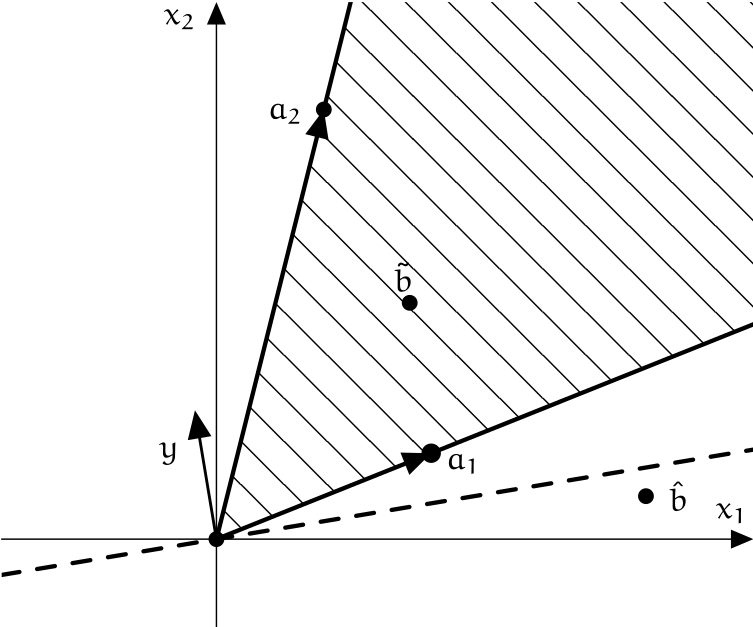
Věta 2.3.9 (Farkas & Minkowski)

Nechť A∈Rm×nA \in \R^{m \times n} a b∈Rmb \in \R^m. Potom je právě jeden z následujících systémů rovnic a nerovnic řešitelný: Ax=b,x≥0,(2.3.5) Ax = b, \quad x \geq 0, \tag{2.3.5} ATy≥0,⟨y,b⟩<0(2.3.6) A^T y \geq 0, \quad \scal y b < 0 \tag{2.3.6}

Jinak řečeno soustava (2.3.5)\tagged{2.3.5} má řešení právě tehdy, když pro všechna y∈Rmy \in \R^m platí ATy≥0A^T y \geq 0 a zároveň ⟨y,b⟩≥0\scal y b \geq 0

Ještě jinak můžeme větu formulovat tak, že buď bb leží v konvexním kuželu cone {ai}i=1n\cone{\brackets{a_i}_{i=1}^n} nebo jsou bb a konvexní kužel silně oddělitelné.

Z této věty pak plynou tzv. věty o alternativě, které můžeme najít například v lineárním programování.

Tvrzení Věty 2.3.9 můžeme také napsat jako:
Jestliže systém f0(x):=⟨a0,x⟩<0,fi(x):=⟨ai,x⟩≤0,i∈{1,…,m} f_0(x) := \scal {a_0} x < 0, \quad f_i(x) := \scal {a_i} x \leq 0, \quad i \in \brackets{1, \dots, m} nemá pro daná a0,…,am∈Rma_0, \dots, a_m \in \R^m řešení na Rn\R^n, pak existují čísla y1,…,ym≥0y_1, \dots, y_m \geq 0 taková, že a0+∑i=1myiai=0,tj. f0(x)+∑i=1myifi(x)=0 a_0 + \sum_{i = 1}^m y_i a_i = 0, \quad \text{tj. }f_0(x) + \sum_{i = 1}^m y_i f_i(x)= 0 pro každé x∈Rnx \in \R^n.

Toto plyne z toho, že pokud v (2.3.9)\tagged{2.3.9} položíme b=a0b = a_0 a A=−(a1,…,am)A = -(a_1, \dots, a_m) (a zaměníme-li xx a yy), pak podle předpokladu nemá systém ATx≥0 & ⟨x,a0⟩<0A^T x \geq 0 \, \and \, \scal x {a_0} < 0 řešení. A tedy dostáváme, že systém Ay=a0,y≥0Ay = a_0, y \geq 0 řešení mít musí.

Věta 2.3.12 (Fan & Glicksburg & Hoffman)

Nechť množina X⊆RnX \subseteq \R^n je konvexní, funkce f1,…,fk:X→Rf_1, \dots, f_k: X \to \R jsou konvexní a funkce fk+1,…,fmf_{k+1}, \dots, f_m afinní, tj. pro j∈{k+1,…,m}j \in \brackets{k+1, \dots, m} máme fj=⟨aj,x⟩+βjf_j = \scal {a_j} x + \beta_j pro vhodná aj∈Rna_j \in \R^n a βj∈R\beta_j \in \R. Jestliže systém nerovností a rovností fi(x)<0,i∈{1,…,k}fj(x)=0,j∈{k+1,…,m}}(2.3.8) \begin{rcases} f_i(x) < 0, & i \in \brackets{1, \dots, k} \\ f_j(x) = 0, & j \in \brackets{k+ 1, \dots, m} \end{rcases} \tag{2.3.8} nemá řešení na XX, pak existují takové konstanty y1,…,yk≥0&yk+1,…,ym∈R y_1, \dots, y_k \geq 0 \quad \and \quad y_{k+1}, \dots, y_m \in \R že pro alespoň jedno l∈{1,…,m}l \in \brackets{1, \dots, m} je yl≠0y_l \neq 0 a pro všechna x∈Xx \in X platí ∑i=1myifi(x)≥0(2.3.9) \sum_{i = 1}^m y_i f_i(x) \geq 0 \tag{2.3.9}

nebo

Následující věta udává podmínky, které zajišťují kladnost jistého význačného yiy_i (BÚNO i=0i = 0) ve vztahu (2.3.9)\tagged{2.3.9}. Po vydělení vztahu (2.3.9)\tagged{2.3.9} tímto yiy_i dostaneme BÚNO yi=1y_i = 1.

Věta 2.3.13 (Podmínky regularity)

Nechť množina X⊆RnX \subseteq \R^n je konvexní a funkce f0,…,fm:X→Rf_0, \dots, f_m: X \to \R jsou konvexní. Jestliže systém nerovností f0(x)<0,(2.3.10) f_0(x) < 0, \tag{2.3.10} fi(x)<0,i∈{1,…,m}(2.3.11) f_i(x) < 0, \quad i \in \brackets{1, \dots, m} \tag{2.3.11} nemá řešení na XX a podsystém (2.3.11)\tagged{2.3.11} má řešení na XX, pak existují y1,…,ym≥0y_1, \dots, y_m \geq 0 taková, že pro všechna x∈Xx \in X platí f0(x)+∑i=1myifi(x)≥0(2.3.12) f_0(x) + \sum_{i = 1}^m y_i f_i(x) \geq 0 \tag{2.3.12}

Back to top