Nutné a postačující podmínky optimality

$$ \xdef\scal#1#2{\langle #1, #2 \rangle} \xdef\norm#1{\left\lVert #1 \right\rVert} \xdef\dist{\rho} \xdef\and{\&}\xdef\brackets#1{\left\{ #1 \right\}} \xdef\parc#1#2{\frac {\partial #1}{\partial #2}} \xdef\mtr#1{\begin{pmatrix}#1\end{pmatrix}} \xdef\bm#1{\boldsymbol{#1}} \xdef\mcal#1{\mathcal{#1}} \xdef\vv#1{\mathbf{#1}}\xdef\vvp#1{\pmb{#1}} \xdef\ve{\varepsilon} \xdef\l{\lambda} \xdef\th{\vartheta} \xdef\a{\alpha} \xdef\Tagged#1{(\text{#1})} \xdef\tagged*#1{\text{#1}} \xdef\tagEqHere#1#2{\href{#2\#eq-#1}{(\text{#1})}} \xdef\tagDeHere#1#2{\href{#2\#de-#1}{\text{#1}}} \xdef\tagEq#1{\href{\#eq-#1}{(\text{#1})}} \xdef\tagDe#1{\href{\#de-#1}{\text{#1}}} \xdef\T#1{\htmlId{eq-#1}{#1}} \xdef\D#1{\htmlId{de-#1}{\vv{#1}}} \xdef\conv#1{\mathrm{conv}\, #1} \xdef\cone#1{\mathrm{cone}\, #1} \xdef\aff#1{\mathrm{aff}\, #1} \xdef\lin#1{\mathrm{Lin}\, #1} \xdef\span#1{\mathrm{span}\, #1} \xdef\O{\mathcal O} \xdef\ri#1{\mathrm{ri}\, #1} \xdef\rd#1{\mathrm{r}\partial\, #1} \xdef\interior#1{\mathrm{int}\, #1} \xdef\proj{\Pi} \xdef\epi#1{\mathrm{epi}\, #1} \xdef\grad#1{\mathrm{grad}\, #1} \xdef\gradT#1{\mathrm{grad}^T #1} \xdef\gradx#1{\mathrm{grad}_x #1} \xdef\hess#1{\nabla^2\, #1} \xdef\hessx#1{\nabla^2_x #1} \xdef\subdif#1{\partial #1} \xdef\co#1{\mathrm{co}\, #1} \xdef\iter#1{^{[#1]}} \xdef\str{^*} \xdef\spv{\mcal V} \xdef\civ{\mcal U} $$

Obecný úvod

Úlohou matematického programování nazveme $$ f(x) \to \min, \quad x \in X \tag{\T{4.1}} $$ kde přípustná množina $X$ je zadána systém rovností a nerovností $$ X := \set{x \in P \subseteq \R^n \mid g_i(x) \leq 0, \; g_j(x) = 0, \; i = 1, \dots, k, \; j = k+1, \dots, m} \tag{\T{4.2}} $$

Zde je důležité podotknout, že vždy chceme nerovnostní omezení pouze tvaru $\bm{g_i(x) \leq 0}$

Je dobré si zapatovat, že

$m$ - počet omezení

$k$ - počet nerovností (tzn. $g_1, \dots, g_k$ jsou nerovnosti, zbytek rovnosti)

Omezení zakomponovaná v $P$ se nazývají přímá, naopak omezení ve formě $g_l$ se nazývají funkcionální. Dále definujme

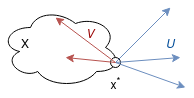
množinu přípustných vektorů
$$\spv(x^* , X) := \set{h \in \lin X \mid \exists \, \a_0 > 0 : x^* + th \in X \text{ pro } \forall t \in (0, \a_0)}$$
- je to kužel
množinu spádových vektorů (kužel zlepšujících vektorů)
$$\civ(x^* , f) := \set{h \in \lin X \mid \exists \, \a_0 > 0 : x^* + th \in D(f) \; \and \; f(x^* + th) < f(x^* ) \text{ pro } \forall t \in (0, \a_0)}$$

Lemma $\D{4.1.1}$

Nechť $X \subseteq \R$ a $f: X \to \R$ jsou dány. Je-li bod $x^* \in X$ lokálním řešením úlohy $\tagEq{4.1}$, potom $$ \spv (x^* , X) \cap \civ (x^* , f) = \emptyset $$

Definice $\D{4.1.2}$ (Stacionární bod)

Nechť množina $X \subseteq \R^n$ je konvexní a funkce $f: X \to \R$ je diferencovatelná na (nějaké otevřené množině obsahující) $X$. Řekneme, že bod $x^* \in X$ je stacionárním bodem úlohy $\tagEq{4.1}$ (nebo také stacionárním bodem funkce $f$ na množině $X$), jestliže $$ \scal {\grad f(x^* )} {x - x^* } \geq 0 \tag{\T{4.1.2}}, $$ pro každé $x \in X$.

Výraz v $\tagEq{4.1.2}$ je směrová derivace $x^* $ do libovolného bodu v $X$ - v těchto směrech musí být $f$ rostoucí

Pro $X = \R^n$ je podmínka $\tagEq{4.1.2}$ splněna pouze v případě $\grad f(x^* ) = 0$

Dále ukažme, že stacionární bod ve smyslu Definice $\tagDe{4.1.2}$ má vlastnosti, které od něj očekáváme.

Věta $\D{4.1.3}$ (Vlastnosti stacionárniho bodu)

Nechť $f: X \to \R$ je diferencovatelná na (nějaké otevřené množině obsahující konvexní množinu) $X \subseteq \R^n$.

Je-li $x^* \in X$ lokálním extrémem funkce $f$ na $X$ (tj. lokálním řešením úlohy $\tagEq{4.1}$), pak $x^* $ je stacionárním bodem funkce $f$ na $X$
Naopak, je-li $f$ (ostře) konvexní na $X$ a $x^* \in X$ je stacionárním bodem $f$ na $X$, pak $x^* $ je (jediným) řešením úlohy $\tagEq{4.1}$, tj. (jediným) globálním minimem $f$ na $X$.

Pokud avšak $f$ není konvexní, potřebujeme o rozhodnutí "extrémnosti" stacionárního bodu další nástroje

Nutná podmínka pro $\tagEq{4.1}$

Je-li $x^* \in X$ lokálním minimem funkce $f: X \to \R, \; f \in C^2$, na konvexní množině $X \subseteq \R^n$, pak $$ (x - x^* )^T \hess f(x^* )(x - x^* ) \geq 0 $$ pro všechna $x \in X$ taková, že $\gradT f(x^* )(x - x^* ) = 0$, tj. pro vektory $(x - x^* )\in \ker\gradT f(x^* )$

Postačující podmínka pro $\tagEq{4.1}$

Bod $x^* $ je lokálním minimem funkce $f: X \to \R, f \in C^2$, na konvexní množině $X \subseteq \R^n$, jestliže $$ \gradT f(x^*) (x - x^*) \geq 0, \; \forall x \in X, $$ (tj. je to stacionární bod ve smyslu Definice $\tagDe{4.1.2}$), množina $X$ je polyedr a platí $$ (x - x^*)^T \hess f(x^*) (x - x^*) > 0 $$ pro všechna $x \in X$ taková, že $x \neq x^* $ a $(x - x^* ) \in \ker \gradT f(x^* )$

Je-li $X$ polyedr, pak je $\spv (x^* , X)$ uzavřená

Nutné a postačující podmínky optimality

Uvažujme přidruženou Lagrangeovu funkci $L: P \times \R \times \R^m \to \R$ k úloze $\tagEq{4.1} \; \and \; \tagEq{4.2}$ definovanou jako $$ L(x, y_0, y) := y_0 f(x) + \sum_{i = 1}^m y_i g_i(x), \tag{\T{4.1.2}}, $$ přičemž v případě $y_0 = 1$ bude $L(x, 1, y) := L(x,y)$. Navíc čísla $y_0, \dots, y_m$ nazyváme Lagrangeovými multiplikátory.

Omezení nazveme aktivní, pokud se realizuje jako rovnost

Dále ještě zaveďme následující $$ Q := \set{y = (y_1, \dots, y_m)^T \mid y_1, \dots, y_k \geq 0} $$ a dvě další množiny:

Množinu aktivních omezení v bodě $x \str$
$$I(x \str) := \set{i \in \set{1, \dots, k} \mid g_i(x \str) = 0}, \quad x \str \in X$$
Množinu indexů všech funkcí, které se v bodě $x\str$ realizují jako rovnost $$S(x \str) := I(x\str) \~~cap~~cup \set{k+1, \dots, m}, \quad x \str \in X$$

Věta $\D{4.2.1}$ (Lagrangeův princip)

Nechť množina $P \subseteq \R^n$ je konvexní, funkce $f, g_1, \dots, g_k : P \to \R$ jsou diferencovatelné v bodě $x^* \in X$ a $g_{k+1}, \dots, g_m$ jsou spojitě diferencovatelné na nějakém okolí bodu $x^* $. Je-li bod $x^* \in X$ lokálním řešením úlohy $\tagEq{4.1} \; \and \; \tagEq{4.2}$, pak existují Lagrangeovy multiplikátory $y_0\str > 0$ a $y\str \in Q$ takové, že ne všechna $y_0 \str, \dots, y_m \str$ jsou nulová a platí $$ \scal {\gradx L(x\str, y_0\str, y\str)} {x - x\str} \geq 0 \quad \forall x \in P \tag{\T{4.2.3}} $$ $$ y_i\str g_i(x\str) = 0, \quad i = 1, \dots, m \tag{\T{4.2.4}} $$

Podmínka $\tagEq{4.2.3}$ znamená, že $x\str$ musí být stacionárním bodem funkce $L(x, y_0\str, y\str)$ (podmínka stacionarity). Dále podmínka $\tagEq{4.2.4}$ se nazývá podmínka komplementarity a požadavek $y_1\str, \dots, y_k\str > 0$ jako podmínka duality.

Jistě $y_0 \str, y_1 \str, \dots, y_k \str \geq 0$, $y_{k+1} \str, \dots, y_m \str \in \R \iff y_0\str > 0$ a $y\str \in Q$

Jelikož situace s $y_0\str = 0$ je problematická, existují podmínky na zaručení $y_0\str \neq 0$, což je ekvivalentní s $y_0\str = 1$. Tyto podmínky se nazývají podmínky kvalifikovaného omezení:

Regulárnost bodu $x\str$, tj, bod $x\str$ je regulární, pokud jsou $\grad g_i(x\str)$ pro $i \in S(x\str)$ lineárně nezávislé (tj. gradienty aktivních omezení jsou LNZ)
afinní omezení - funkce $g_1, \dots, g_m$ jsou afinní
Slaterova podmínka - $g_1, \dots, g_k$ jsou konvexní, $g_{k+1}, \dots, g_m$ jsou afinní, pokračuje, ale viz $\tagDe{4.2.3}$

Důsledek $\D{4.2.2}$

Nechť $P \subseteq \R^n$ je konvexní množina, funkce $f, g_1, \dots, g_m$ jsou diferencovatelné na (nějaké otevřené množině obsahující) $P$ a pro $x\str \in X$ existují multiplikátory $y\str \in Q$ takové, že platí $\tagEq{4.2.3}$ & $\tagEq{4.2.4}$ s $y_0\str = 1$. Nechť je dále splněn (alespoň) jeden z následujících předpokladů:

funkce $L(x, y\str)$ je konvexní na množině $P$
úloha $\tagEq{4.1}$ & $\tagEq{4.2}$ je úlohou konvexního programování, tj. na konvexní množině $P$ jsou funkce $f, g_1, \dots, g_k$ konvexní a $g_{k+1}, \dots, g_m$ afinní

Pak bod $x\str$ je globálním řešením úlohy $\tagEq{4.1}$ & $\tagEq{4.2}$.

Teoreticky stačí pouze kvazikonvexní $g_1, \dots, g_k$

Věta $\D{4.2.3}$ (Karushova-Kuhnova-Tuckerova v diferenciálním tvaru)

Nechť $P \subseteq \R^n$ je konvexní množina, funkce $f, g_1, \dots, g_k$ konvexní a diferencovatelné na (nějaké otevřené množině obsahující) $P$, funkce $g_{k+1}, \dots, g_m$ afinní na $P$ a nechť platí (alespoň) jedna z následujících podmínek:

(LNZ) množina $P$ je otevřená, vektory $\grad g_i(x), i \in S(x)$ jsou lineárně nezávislé pro každé $x \in X$.
(Slaterova) funkcionální omezení jsou pouze tvaru nerovností, tj. $k = m$, a existuje bod $\bar x \in P$ takový, že $g_i(\bar x) < 0$ pro $i \in \set{1, \dots, k}$
(lineární) množina $P$ je polyedr a funkce $g_1, \dots, g_k$ jsou afinní

Pak $x\str$ je řešením úlohy $\tagEq{4.1}$ & $\tagEq{4.2}$ právě tehdy, když existuje $y\str \in Q$ takové, že platí $\tagEq{4.2.3}$ & $\tagEq{4.2.4}$ s $y_0\str = 1$.

Věta $\D{4.2.4}$

Nechť funkce $f, g_1, \dots, g_m$ jsou dvakrát spojitě diferencovatelné v bodě $x\str$ a $x\str \in \interior P$ je takový, že existují multiplikátory $y\str \in Q$ splňující $\tagEq{4.2.3}$ & $\tagEq{4.2.4}$ s $y_0\str = 1$ a současně $y_i\str > 0$ pro $i \in I(x\str)$ (tzv. podmínka ostré komplementarity), tj. $$ \gradx L(x\str, y\str) = 0, $$ $$ g_i(x\str) \leq 0 \text{ pro } i \in \set{1, \dots, k}, \qquad g_i(x\str) = 0 \text{ pro } i \in \set{k+1, \dots, m}, $$ $$ y_i\str > 0 \text{ pro } i \in I(x\str), \qquad y_i\str = 0 \text{ pro } i \in \set{1, \dots, k} \setminus I(x\str), $$ $$ y_i\str \in \R \text{ pro } i \in \set{k+1, \dots, m} $$ Jestliže $$ \hessx L(x\str, y\str) > 0 \text{ na } \ker (\gradT g_i(x\str))_{i \in S(x\str)}, $$ tj. $h^T \hessx L(x\str, y\str) h > 0$ pro všechna $h \in \R^n \setminus \brackets{0}$ taková, že $\scal {\grad g_i(x\str)} h = 0$ pro $i \in S(x\str)$, pak bod $x\str$ je ostré lokální minimum funkce $f$ na množině $X$.