Nutné a postačující podmínky optimality
$$ \xdef\scal#1#2{\langle #1, #2 \rangle} \xdef\norm#1{\left\lVert #1 \right\rVert} \xdef\dist{\rho} \xdef\and{\&}\xdef\brackets#1{\left\{ #1 \right\}} \xdef\parc#1#2{\frac {\partial #1}{\partial #2}} \xdef\mtr#1{\begin{pmatrix}#1\end{pmatrix}} \xdef\bm#1{\boldsymbol{#1}} \xdef\mcal#1{\mathcal{#1}} \xdef\vv#1{\mathbf{#1}}\xdef\vvp#1{\pmb{#1}} \xdef\ve{\varepsilon} \xdef\l{\lambda} \xdef\th{\vartheta} \xdef\a{\alpha} \xdef\Tagged#1{(\text{#1})} \xdef\tagged*#1{\text{#1}} \xdef\tagEqHere#1#2{\href{#2\#eq-#1}{(\text{#1})}} \xdef\tagDeHere#1#2{\href{#2\#de-#1}{\text{#1}}} \xdef\tagEq#1{\href{\#eq-#1}{(\text{#1})}} \xdef\tagDe#1{\href{\#de-#1}{\text{#1}}} \xdef\T#1{\htmlId{eq-#1}{#1}} \xdef\D#1{\htmlId{de-#1}{\vv{#1}}} \xdef\conv#1{\mathrm{conv}\, #1} \xdef\cone#1{\mathrm{cone}\, #1} \xdef\aff#1{\mathrm{aff}\, #1} \xdef\lin#1{\mathrm{Lin}\, #1} \xdef\span#1{\mathrm{span}\, #1} \xdef\O{\mathcal O} \xdef\ri#1{\mathrm{ri}\, #1} \xdef\rd#1{\mathrm{r}\partial\, #1} \xdef\interior#1{\mathrm{int}\, #1} \xdef\proj{\Pi} \xdef\epi#1{\mathrm{epi}\, #1} \xdef\grad#1{\mathrm{grad}\, #1} \xdef\hess#1{\nabla^2\, #1} \xdef\subdif#1{\partial #1} \xdef\co#1{\mathrm{co}\, #1} \xdef\iter#1{^{[#1]}} \xdef\spv{\mcal V} \xdef\civ{\mcal U} $$
Úlohou matematického programování nazveme $$ f(x) \to \min, \quad x \in X \tag{\T{4.1}} $$ kde přípustná množina $X$ je zadána systém rovností a nerovností $$ X := \set{x \in P \subseteq \R^n \mid g_i(x) \leq 0, \; g_j(x) = 0, \; i = 1, \dots, k, \; j = k+1, \dots, m} \tag{\T{4.2}} $$
Omezení zakomponovaná v $P$ se nazývají příma, naopak omezení ve formě $g_l$ se nazývají funkcionální. Dále definujme
-
množinu přípustných vektorů
$$\spv(x^* , X) := \set{h \in \lin X \mid \exists \, \a_0 > 0 : x^* + th \in X \text{ pro } \forall t \in (0, \a_0)}$$ -
množinu spádových vektorů (kužel zlepšujících vektorů)
$$\civ(x^* , f) := \set{h \in \lin X \mid \exists \, \a_0 > 0 : x^* + th \in D(f) \; \and \; f(x^* + th) < f(x^* ) \text{ pro } \forall t \in (0, \a_0)}$$
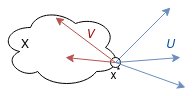
Jistě tedy platí $$ \spv (x^* , X) \cap \civ(x^* , f) = \emptyset $$
