Konvexní funkce

$$ \xdef\scal#1#2{\langle #1, #2 \rangle} \xdef\norm#1{\left\lVert #1 \right\rVert} \xdef\dist{\rho} \xdef\and{\&}\xdef\brackets#1{\left\{ #1 \right\}} \xdef\parc#1#2{\frac {\partial #1}{\partial #2}} \xdef\mtr#1{\begin{pmatrix}#1\end{pmatrix}} \xdef\bm#1{\boldsymbol{#1}} \xdef\mcal#1{\mathcal{#1}} \xdef\vv#1{\mathbf{#1}}\xdef\vvp#1{\pmb{#1}} \xdef\ve{\varepsilon} \xdef\l{\lambda} \xdef\th{\vartheta} \xdef\a{\alpha} \xdef\tagged#1{(\text{#1})} \xdef\tagEq#1{\href{\#eq-#1}{(\text{#1})}} \xdef\tagDe#1{\href{\#de-#1}{\text{#1}}} \xdef\T#1{\htmlId{eq-#1}{#1}} \xdef\D#1{\htmlId{de-#1}{\vv{#1}}} \xdef\conv#1{\mathrm{conv}\, #1} \xdef\cone#1{\mathrm{cone}\, #1} \xdef\aff#1{\mathrm{aff}\, #1} \xdef\lin#1{\mathrm{Lin}\, #1} \xdef\span#1{\mathrm{span}\, #1} \xdef\O{\mathcal O} \xdef\ri#1{\mathrm{ri}\, #1} \xdef\rd#1{\mathrm{r}\partial\, #1} \xdef\interior#1{\mathrm{int}\, #1} \xdef\proj{\Pi} \xdef\epi#1{\mathrm{epi}\, #1} \xdef\grad#1{\mathrm{grad}\, #1} \xdef\hess#1{\nabla^2\, #1} $$

Definice $\D{2.2.1}$ (Konvexní funkce)

Nechť $X \subseteq \R^n$ je konvexní množina. Funkce $f: X \to \R$ se nazývá

konvexní na $X$, jestliže pro všechna $x_1, x_2 \in X$ a každé $\l \in [0,1]$ platí
$$f(\l x_1 + (1 - \l)x_2) \leq \l f(x_1) + (1-\l) f(x_2) \tag{\T{2.2.1}}$$
ostře konvexní na $X$, jestliže nerovnost $\tagEq{2.2.1}$ je ostrá pro všechna $x_1, x_2 \in X, x_1 \neq x_2$ a každé $\l \in (0,1)$.
silně konvexní na $X$ s konstantou silné konvexnosti $\th > 0$, jestliže pro všechna $x_1, x_2 \in X$ a každé $\l \in [0,1]$ platí
$$\underbrace{f(\l x_1 + (1 - \l)x_2) \leq \l f(x_1) + (1 - \l) f(x_2)}_{\tagEq{2.2.1}} - \th \l(1-\l)\norm{x_1 - x_2}^2 \tag{\T{2.2.2}}$$

V praxi je silná konvexnost "silnější" než ostrá konvexnost a ta je silnější než "obyčejná" konvexnost

Věta $\D{2.2.2}$ (Konvexnost nadgrafu)

Nechť $X \subseteq \R^n$ je konvexní množina a nechť $f : X \to \R$. Funkce $f$ je konvexní na $X$ právě tehdy, když její nadgraf (epigraf) $$ \epi f := \brackets{\underbrace{[x, \beta]}_{\text{bod}} \in \R^{n+1} \mid x \in X, \beta \geq f(x)} $$ je konvexní množina.

Pro ostře konvexní funkci musí "tyto dva body" vždy ležet nad sebou (myšleny jejich souřadnice na ose $y$). Navíc pro silnou konvexnost mezi nimi musí vždy být alespoň daná mezera.

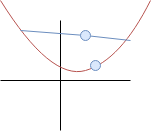
Tyto body nemusí ležet nad sebou (na svislé přímce). Navíc ještě

$f$ konvexní $\iff$ $-f$ konkávní

Kombinace konvexních funkcí

Věta $\D{2.2.3}$ (Nezáporná linearní kombinace konvexních funkcí)

Nechť $X \subseteq \R^n$ je konvexní množina, funkce $f_1, \dots, f_m: X \to \R$ jsou konvexní na $X$ a $\a_1, \dots, \a_m \geq 0$ jsou daná čísla. Potom $F(x) = \a_1 f_1(x) + \dots + \a_m f_m(x)$ je konvexní.

Věta $\D{2.2.4}$ (Sublevel set)

Nechť $X \subseteq \R^n$ je konvexní množina a $f: X \to \R$ je konvexní funkce na $X$. Pak pro libovolné $K \in \R$ je odpovídající dolní vrstevnicová množina (sublevel set) $$ V_K := \brackets{x \in X \mid f(x) \leq K} $$ také konvexní.

Platí pouze tato implikace: $f$ konvexní $\implies$ sublevel set konvexní
Například $x^3$ má konvexní sublevel set, ale sama konvexní není.

Přesněji říkáme, že pokud má funkce $f$ konvexní sublevel set, pak $f$ je kvazikonvexní.

Věta $\D{2.2.5}$ (Jensen)

Nechť $X \subseteq \R^n$ je konvexní množina a funkce $f:X \to \R$ je konvexní na $X$. Pak pro libovolné $m \in \N, x_1, \dots, x_m \in X$ a čísla $\l_1, \dots, \l_m \geq 0$ splňující $\sum_{i = 1}^m \l_i = 1$ platí $$ f \left( \sum_{i = 1}^m \l_i x_i \right) \leq \sum_{i = 1}^m \l_i f(x_i). \tag{\T{2.2.3}} $$ Je-li navíc funkce $f$ ostře konvexní a $\l_1, \dots, \l_m \in (0,1)$, pak rovnost v $\tagEq{2.2.3}$ nastane právě tehdy, když $x_1 = \dots = x_m$.

První část Věty $\tagDe{2.2.5}$ lze jistě podle Definice $\tagDe{2.2.1}$ nahradit ekvivalencí

Z Jensenovy nerovnosti $\tagEq{2.2.3}$ lze odvodit například AG nerovnost
$${x_1 + \dots + x_m \over m} \leq \sqrt[m]{x_1 \cdot \ldots \cdot x_m}$$

Lokalizace minima konvexní funkce

Věta $\D{2.2.6}$

Nechť $X \subseteq \R^n$ je konvexní množina a funkce $f: X \to \R$ konvexní. Potom následující tvrzení jsou pravdivá

Libovolné lokální minimum funkce $f$ na $X$ je současně globálním minimem.
Množina bodů množiny $X$, v nichž funkce $f$ nabývá svého minima na $X$, je konvexní. Je-li funkce dokonce ostře konvexní, pak je tato množina nejvýše jednoprvková.
Je-li funkce $f$ diferencovatelná na otevřené množině $\mcal U \supseteq X$ a $x^* \in X$ je jejím stacionárním bodem, tj. $\grad f(x^* ) = 0$, pak $x^* $ je bodem globálního minima funkce $f$ na množině $X$.

Z Věty $\tagDe{2.2.6}$ mimo jiné plyne, že je-li $f: X \to \R$ (ostře) konvexní a spojitá funkce na konvexní a kompaktní množině $X \subseteq \R^n$, pak $f$ má na $X$ (právě jedno) globální minumum.

Věta $\D{2.2.7}$ (Základní věta konvexního programování)

Máme-li konvexní funkci $f: X \to \R$ na polytopu $X := \conv \brackets{x_1, \dots, x_m} \subseteq \R^n$, pak je maximum funkce $f$ na $X$ dosaženo v některém z bodů $x_1, \dots, x_m$.

Obecněji: je-li $X$ konvexní a kompaktní množina, pak maximum nastává v extrémním bodě (tj. v takovém bodě, který není netriviální konvexní kombinací dvou bodů z $X$)

Z Věty $\tagDe{2.2.7}$ plyne základní věta lineárního programování:
Je-li funkce $f$ afinní (taková funkce je konvexní i konkávní zároveň), pak globální maximum nastává v některém z bodů $x_1, \dots, x_m$, tj. v některém z "vrcholů" polytopu.

Vlastnosti konvexních funkcí

Věta $\D{2.4.1}$ (Spojitost konvexní funkce)

Nechť $X \subseteq \R^n$ je konvexní množina a funkce $f: X \to \R$ je konvexní na $X$. Pak $f$ je spojitá pro každé $x \in \ri X$.

Dále ještě známe několik podmínek zaručujících ~~spojitost~~konvexnost funkce $f: \R \to \R$:

má-li $f$ vlastní derivaci v otevřeném intervalu $I$, pak $f$ je (ostře) konvexní na $I$ právě tehdy, když $f'$ je neklesající (rostoucí) na $I$.
má-li $f$ vlastní derivaci v otevřeném intervalu $I$, pak $f$ je (ostře) konvexní na $I$ právě tehdy, když pro každé $x, x^* \in I$ platí
$$f(x) \geq^{(>)} f(x^* ) + f'(x^* )(x - x^* ),$$ tj. graf funkce $f$ leží nad tečnou sestrojenou v libovolném bodě.
má-li $f$ vlastní druhou derivaci v otevřeném intervalu $I$, pak $f$ je konvexní na $I$ právě tehdy, když funkce $f''(x) \geq 0$ (je-li $f''(x) > 0$ na $I$, pak ostře konvexní)

Tyto tvrzení si nyní rozšiřme pro $f: \R^n \to \R$ pro silnou konvexnost s konstatnou $\th$ (volbou $\th = 0$ dostáváme ostrou konvexnost)

Věta $\D{2.4.2}$

Nechť $X \subseteq \R^n$ je konvexní množina a funkce $f$ diferencovatelná na otevřené množině $\mcal U \supseteq X$. Pak $f$ je silně konvexní na $X$ s konstantou silné konvexnosti $\th \geq 0$ právě tehdy, když pro každé $x, x^* \in X$ platí $$ f(x) \geq f(x^* ) + \scal {\grad f(x^* )} {x - x^* } + \th \norm{x - x^* }^2 \tag{\T{2.4.1}} $$

Ve $\tagEq{2.4.1}$ výraz $\scal {\grad f(x^* )} {x - x^* }$ hraje úlohu tečné nadroviny v bodě $x^* $ s normálovým vektorem $\grad f(x^* )$ (tečným jak na nadrovinu, tak na funkci $f$ v bodě $x^* $)

Důsledek $\D{2.4.5}$

Nechť $X \subseteq \R^n$ je konvexní množina splňující $\interior X \neq \emptyset$. Nechť funkce $f: X \to \R$ je dvakrát spojitě diferencovatelná na otevřené množině $\mcal U \supseteq X$ s maticí druhých derivací $\hess f(x)$ (Hessova matice). Pak $f$ je silně konvexní na $X$ s konstantou silné konvexnosti $\th \geq 0$ právě tehdy, když pro každé $x \in X$ a $h \in \R^n$ platí $$ \scal {\hess f(x)} h \geq 2 \th \norm{h}^2 \tag{\T{2.4.3}}, $$ jinými slovy $\hess f(x) \geq 2 \th I$ pro všechna $x \in X$.

Z Důsledku $\tagDe{2.4.5}$ plynou následující tři implikace

$\hess f(x) \geq 0$ pro všechna $x \in X \implies f$ je konvexní na $X$
$\hess f(x) > 0$ pro všechna $x \in X \implies f$ je ostře konvexní na $X$
$\interior X \neq \emptyset$ a $f$ je konvexní na $X \implies \hess f(x) \geq 0$ pro všechna $x \in X$