Konvexní funkce
$$ \xdef\scal#1#2{\langle #1, #2 \rangle} \xdef\norm#1{\left\lVert #1 \right\rVert} \xdef\dist{\rho} \xdef\and{\&}\xdef\brackets#1{\left\{ #1 \right\}} \xdef\parc#1#2{\frac {\partial #1}{\partial #2}} \xdef\mtr#1{\begin{pmatrix}#1\end{pmatrix}} \xdef\bm#1{\boldsymbol{#1}} \xdef\mcal#1{\mathcal{#1}} \xdef\vv#1{\mathbf{#1}}\xdef\vvp#1{\pmb{#1}} \xdef\ve{\varepsilon} \xdef\l{\lambda} \xdef\th{\vartheta} \xdef\a{\alpha} \xdef\tagged#1{\href{\#eq-#1}{(\text{#1})}} \xdef\teq#1{\htmlId{eq-#1}{#1}} \xdef\conv#1{\mathrm{conv}\, #1} \xdef\cone#1{\mathrm{cone}\, #1} \xdef\aff#1{\mathrm{aff}\, #1} \xdef\lin#1{\mathrm{Lin}\, #1} \xdef\span#1{\mathrm{span}\, #1} \xdef\O{\mathcal O} \xdef\ri#1{\mathrm{ri}\, #1} \xdef\rd#1{\mathrm{r}\partial\, #1} \xdef\interior#1{\mathrm{int}\, #1} \xdef\proj{\Pi} \xdef\epi#1{\mathrm{epi}\, #1} \xdef\grad#1{\mathrm{grad}\, #1} $$
Definice 2.2.1 (Konvexní funkce)
Nechť $X \subseteq \R^n$ je konvexní množina. Funkce $f: X \to \R$ se nazývá
-
konvexní na $X$, jestliže pro všechna $x_1, x_2 \in X$ a každé $\l \in [0,1]$ platí
$$f(\l x_1 + (1 - \l)x_2) \leq \l f(x_1) + (1-\l) f(x_2) \tag{\teq{2.2.1}}$$ - ostře konvexní na $X$, jestliže nerovnost $\tagged{2.2.1}$ je ostrá pro všechna $x_1, x_2 \in X, x_1 \neq x_2$ a každé $\l \in (0,1)$.
-
silně konvexní na $X$ s konstantou silné konvexnosti $\th > 0$, jestliže pro všechna $x_1, x_2 \in X$ a každé $\l \in [0,1]$ platí
$$\underbrace{f(\l x_1 + (1 - \l)x_2) \leq \l f(x_1) + (1 - \l) f(x_2)}_{\tagged{2.2.1}} - \th \l(1-\l)\norm{x_1 - x_2}^2 \tag{2.2.2}$$
V praxi je silná konvexnost "silnější" než ostrá konvexnost a ta je silnější než "obyčejná" konvexnost
Věta 2.2.2 (Konvexnost nadgrafu)
Nechť $X \subseteq \R^n$ je konvexní množina a nechť $f : X \to \R$. Funkce $f$ je konvexní na $X$ právě tehdy, když její nadgraf (epigraf) $$ \epi f := \brackets{\underbrace{[x, \beta]}_{\text{bod}} \in \R^{n+1} \mid x \in X, \beta \geq f(x)} $$ je konvexní množina.
Pro ostře konvexní funkci musí "tyto dva body" vždy ležet nad sebou. Navíc pro silnou konvexnost mezi nimi musí vždy být alespoň daná mezera.
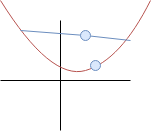
Tyto body nemusí ležet nad sebou (na svislé přímce). Navíc ještě
$f$ konvexní $\iff$ $-f$ konkávní
Věta 2.2.3 (Nezáporná linearní kombinace konvexních funkcí)
Nechť $X \subseteq \R^n$ je konvexní množina, funkce $f_1, \dots, f_m: X \to \R$ jsou konvexní na $X$ a $\a_1, \dots, \a_m \geq 0$ jsou daná čísla. Potom $F(x) = \a_1 f_1(x) + \dots + \a_m f_m(x)$ je konvexní.
Věta 2.2.4 (Sublevel set)
Nechť $X \subseteq \R^n$ je konvexní množina a $f: X \to \R$ je konvexní funkce na $X$. Pak pro libovolné $K \in \R$ je odpovídající dolní vrstevnicová množina (sublevel set) $$ V_K := \brackets{x \in X \mid f(x) \leq K} $$ také konvexní.
Platí pouze tato implikace: $f$ konvexní $\implies$ sublevel set konvexní
Například $x^3$ má konvexní sublevel set, ale sama konvexní není.
Přesněji říkáme, že pokud má funkce $f$ konvexní sublevel set, pak $f$ je kvazikonvexní.
Věta 2.2.5 (Jensen)
Nechť $X \subseteq \R^n$ je konvexní množina a funkce $f:X \to \R$ je konvexní na $X$. Pak pro libovolné $m \in \N, x_1, \dots, x_m \in X$ a čísla $\l_1, \dots, \l_m \geq 0$ splňující $\sum_{i = 1}^m \l_i = 1$ platí $$ f \left( \sum_{i = 1}^m \l_i x_i \right) \leq \sum_{i = 1}^m \l_i f(x_i). \tag{2.2.3} $$ Je-li navíc funkce $f$ ostře konvexní a $\l_1, \dots, \l_m \in (0,1)$, pak rovnost v $\tagged{2.2.3}$ nastane právě tehdy, když $x_1 = \dots = x_m$.
První část Věty 2.2.5 lze jistě podle Definice 2.2.1 nahradit ekvivalencí
Z Jensenovy nerovnosti $\tagged{2.2.3}$ lze odvodit například AG nerovnost
$${x_1 + \dots + x_m \over m} \leq \sqrt[m]{x_1 \cdot \ldots \cdot x_m}$$
Věta 2.2.6
Nechť $X \subseteq \R^n$ je konvexní množina a funkce $f: X \to \R$ konvexní. Potom následující tvrzení jsou pravdivá
- Libovolné lokální minimum funkce $f$ na $X$ je současně globálním minimem.
- Množina bodů množiny $X$, v nichž funkce $f$ nabývá svého minima na $X$, je konvexní. Je-li funkce dokonce ostře konvexní, pak je tato množina nejvýše jednoprvková.
- Je-li funkce $f$ diferencovatelná na otevřené množině $\mcal U \supseteq X$ a $x^* \in X$ je jejím stacionárním bodem, tj. $\grad f(x^* ) = 0$, pak $x^* $ je bodem globálního minima funkce $f$ na množině $X$.
$\tagged{2.2.2}$