Skip to main content

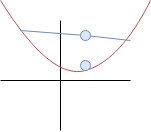
Konvexní funkce

$$ \xdef\scal#1#2{\langle #1, #2 \rangle} \xdef\norm#1{\left\lVert #1 \right\rVert} \xdef\dist{\rho} \xdef\and{\&}\xdef\brackets#1{\left\{ #1 \right\}} \xdef\parc#1#2{\frac {\partial #1}{\partial #2}} \xdef\mtr#1{\begin{pmatrix}#1\end{pmatrix}} \xdef\bm#1{\boldsymbol{#1}} \xdef\vv#1{\mathbf{#1}}\xdef\vvp#1{\pmb{#1}} \xdef\ve{\varepsilon} \xdef\l{\lambda} \xdef\th{\vartheta} \xdef\a{\alpha} \xdef\tagged#1{(\text{#1})} \xdef\conv#1{\mathrm{conv}\, #1} \xdef\cone#1{\mathrm{cone}\, #1} \xdef\aff#1{\mathrm{aff}\, #1} \xdef\lin#1{\mathrm{Lin}\, #1} \xdef\span#1{\mathrm{span}\, #1} \xdef\O{\mathcal O} \xdef\ri#1{\mathrm{ri}\, #1} \xdef\rd#1{\mathrm{r}\partial\, #1} \xdef\interior#1{\mathrm{int}\, #1} \xdef\proj{\Pi} \xdef\epi#1{\mathrm{epi}\, #1} $$

Definice 2.2.1 (Konvexní funkce)

Nechť $X \subseteq \R^n$ je konvexní množina. Funkce $f: X \to \R$ se nazývá

  • konvexní na $X$, jestliže pro všechna $x_1, x_2 \in X$ a každé $\l \in [0,1]$ platí
    $$f(\l x_1 + (1 - \l)x_2) \leq \l f(x_1) + (1-\l) f(x_2) \tag{2.2.1}$$
  • ostře konvexní na $X$, jestliže nerovnost $\tagged{2.2.1}$ je ostrá pro všechna $x_1, x_2 \in X, x_1 \neq x_2$ a každé $\l \in (0,1)$.
  • silně konvexní na $X$ s konstantou silné konvexnosti $\th > 0$, jestliže pro všechna $x_1, x_2 \in X$ a každé $\l \in [0,1]$ platí
    $$\underbrace{f(\l x_1 + (1 - \l)x_2) \leq \l f(x_1) + (1 - \l) f(x_2)}_{\tagged{2.2.1}} - \th \l(1-\l)\norm{x_1 - x_2}^2 \tag{2.2.2}$$

V praxi je silná konvexnost "silnější" než ostrá konvexnost a ta je silnější než "obyčejná" konvexnost

Věta 2.2.2 (Konvexnost nadgrafu)

Nechť $X \subseteq \R^n$ je konvexní množina a nechť $f : X \to \R$. Funkce $f$ je konvexní na $X$ právě tehdy, když její nadgraf (epigraf) $$ \epi f := \brackets{\underbrace{[x, \beta]}_{\text{bod}} \in \R^{n+1} \mid x \in X, \beta \geq f(x)} $$ je konvexní množina.

Back to top