Analýza citlivosti
$$ \xdef\scal#1#2{\langle #1, #2 \rangle} \xdef\norm#1{\left\lVert #1 \right\rVert} \xdef\dist{\rho} \xdef\and{\&}\xdef\brackets#1{\left\{ #1 \right\}} \xdef\parc#1#2{\frac {\partial #1}{\partial #2}} \xdef\mtr#1{\begin{pmatrix}#1\end{pmatrix}} \xdef\bm#1{\boldsymbol{#1}} \xdef\mcal#1{\mathcal{#1}} \xdef\vv#1{\mathbf{#1}}\xdef\vvp#1{\pmb{#1}} \xdef\ve{\varepsilon} \xdef\l{\lambda} \xdef\th{\vartheta} \xdef\a{\alpha} \xdef\vf{\varphi} \xdef\Tagged#1{(\text{#1})} \xdef\tagged*#1{\text{#1}} \xdef\tagEqHere#1#2{\href{#2\#eq-#1}{(\text{#1})}} \xdef\tagDeHere#1#2{\href{#2\#de-#1}{\text{#1}}} \xdef\tagEq#1{\href{\#eq-#1}{(\text{#1})}} \xdef\tagDe#1{\href{\#de-#1}{\text{#1}}} \xdef\T#1{\htmlId{eq-#1}{#1}} \xdef\D#1{\htmlId{de-#1}{\vv{#1}}} \xdef\conv#1{\mathrm{conv}\, #1} \xdef\cone#1{\mathrm{cone}\, #1} \xdef\aff#1{\mathrm{aff}\, #1} \xdef\lin#1{\mathrm{Lin}\, #1} \xdef\span#1{\mathrm{span}\, #1} \xdef\O{\mathcal O} \xdef\ri#1{\mathrm{ri}\, #1} \xdef\rd#1{\mathrm{r}\partial\, #1} \xdef\interior#1{\mathrm{int}\, #1} \xdef\proj{\Pi} \xdef\epi#1{\mathrm{epi}\, #1} \xdef\grad#1{\mathrm{grad}\, #1} \xdef\gradT#1{\mathrm{grad}^T #1} \xdef\gradx#1{\mathrm{grad}_x #1} \xdef\hess#1{\nabla^2\, #1} \xdef\hessx#1{\nabla^2_x #1} \xdef\jacobx#1{D_x #1} \xdef\jacob#1{D #1} \xdef\subdif#1{\partial #1} \xdef\co#1{\mathrm{co}\, #1} \xdef\iter#1{^{[#1]}} \xdef\str{^*} \xdef\spv{\mcal V} \xdef\civ{\mcal U} \xdef\knvxProg{\tagEqHere{4.1}{./nutne-a-postacujici-podminky-optimality} \, \and \, \tagEqHere{4.2}{nutne-a-postacujici-podminky-optimality}} $$
Nyní se budeme věnovat řešení úlohy matematické programování v závislosti na parametru.
První se podíváme na úlohu matematické programování s omezeními pouze ve tvaru rovností, ale s obecnou závislostí na parametrech.
A v druhém (a posledním) případě se podíváme na úlohu s omezeními ve tvaru nerovností, ale s parametry pouze v podobě absolutních členů ve funkcích zadávajících tyto omezení.
Zde je dobré podotknout, že druhý případ je mírně užitečnější a navíc si uvědomme, že 1 rovnost lze napsat jako 2 nerovnosti
Úlohy s rovnostmi
Věta $\D{4.4.1}$ (O obálce)
Mějme úlohu $$ f(x,r) \to \min, \qquad g_1(x, r) = 0, \; \dots, \; g_m(x,r) = 0 \tag{\T{AC.1}} $$ kde $x \in \R^n, r \in \R^k, f, g_1, \dots, g_m \in C^1$. Připusťme, že pro každou hodnotu parametru $r$ má úloha $\tagEq{AC.1}$ jediné řešení, které označíme $x\str (r)$. Potom hodnota úlohy $\tagEq{AC.1}$ je $$ f\str(r) = f(x\str(r), r). $$ Je-li $x\str(r)$ diferencovatelná vzhledem k $r$ a Jacobiho matice $\jacobx G(x\str (r), r) \in \R^{m\times n}$ má plnou hodnost $m$, pak platí $$ \parc {} {r_i}f\str(r) = \parc f {r_i} (x\str(r), r) + \sum_{j = 1}^m y_j\str(r) \parc {g_j} {r_i} (x\str(r), r) $$
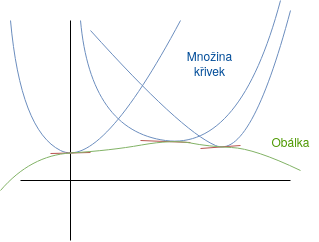
Obálka je křivka, která se množiny křivek dotýká (tj. se dotýká každé křívky) a má společnou tečnu s danou křivkou
Jinak řečeno je tečná k množině křivek
Požadavky Věty $\tagDe{4.4.1}$ jsou relativně silné, proto uveďme její "slabší verzi".
Věta $\D{4.4.2}$
Nechť $f, g_1, \dots, g_m \in C^2$ a $x\str$ je lokálním řešením úlohy $$ f(x) \to \min, \qquad g_1(x) = 0, \dots, g_m(x) = 0 $$ s odpovídajícími Lagrangeovými multiplikátory $y\str$. Nechť dále tato dvojice splňuje postačující podmínku druhého řádu, tj. $\hessx L(x\str, y\str) > 0$ na $\ker \jacob G(x\str)$, přičemž současně $x\str$ je regulárním bodem, tj. $\jacobx G(x\str) \in \R^{m\times n}$ má plnou hodnost $m$. Uvažme úlohu parametrického programování $$ f(x) \to \min, \qquad G(x) = u \tag{\T{AC.2}}, $$ pro parametr $u \in \R^m$. Pak existuje otevřená koule $S$ se středem v počátku ($u = 0$) taková, že pro každé $u \in S$ existuje lokální řešení $x\str(u) \in \R^n$ úlohy $\tagEq{AC.2}$ a odpovídající $y\str(u) \in \R^m$. Navíc $x\str(\cdot)$ a $y\str(\cdot)$ jsou spojitě diferencovatelné funkce na $S$ a platí $x\str(0) = x\str, y\str(0) = y\str$ a pro každé $u \in S$ máme $$ \grad f\str(u) = - y\str(u), $$ kde $f\str(u)$ značí optimální hodnotu úlohy $\tagEq{AC.2}$ vzhledem k $u$, tj. klademe $f\str(u) := f(x\str(u))$.
Jednoduše řečeno se optimální hodnota mění podle Lagrangeových multiplikátorů pro danou hodnotu $u$
Úlohy s nerovnostmi
Uvažujme úlohu závislou na $m$-tici parametrů $b = (b_1, \dots, b_m)^T \in \R^m$, tj. $$ f(x) \to \min, \qquad x \in X(b) := \set{x \in P \subseteq \R^n \mid g_i(x) \leq b_i, \; i \in \set{1, \dots, m}} \tag{\T{4.4.2}} $$ A dále zaveďme značení $$ G(x) := (g_1(x), \dots, g_m(x))^T, \quad X(b) := \set{x \in P \mid G(x) \leq b} $$ $$ B := \set{b \in \R^m \mid X(b) \neq \emptyset}, \quad F(b) := \inf_{x \in X(b)} f(x), \; b \in B $$ množinu K-T vektorů úlohy $\tagEq{4.4.2}$ označme $$ Y(b) := \set{y \in \R^m \mid y \geq 0, \; F(b) \leq f(x) + \scal{y} {G(x) - b} \; \forall x \in P} $$ a subdifereniál funkce $F(b)$ (viz Definice $\tagDeHere{2.5.1}{./subgradient-a-subdiferencial-a-fenchelova-transformace}$) označme $$ \subdif F(b) := \set{a \in \R^m \mid F(b') - F(b) \geq \scal a {b' - b} \; \forall b' \in B} $$
Věta $\D{4.4.3}$
Nechť množina $P \subseteq \R^n$ je konvexní, funkce $f, g_1, \dots, g_m$ jsou konvexní na $P$ a platí $0 \in B, F(0) > -\infty$ a $Y(0) \neq \emptyset$. Potom
- množina $B$ je konvexní
- funkce $F(b)$ je konečná, konvexní a nerostoucí na $B$
- platí $\subdif F(b) = -Y(b)$ pro všechna $b \in B$
Z předpokladů Věty $\tagDe{4.4.3}$ plyne, že
- úloha $\tagEq{4.4.2}$ je přípustná pro $b = 0$
- úloha $\tagEq{4.4.2}$ má řešení pro $b = 0$
- množina K-T vektorů úlohy $\tagEq{4.4.2}$ je neprázdná (toto není splněno automaticky, viz Věta $\tagDeHere{4.3.2}{./dualni-uloha}$)
Navíc je-li $F$ dokonce diferencovatelná v $b$, pak $\subdif F(b)$ je jednoprvková množina, která obsahuje pouze $-\gradT F(b)$ a tedy tento vektor musí být roven $(-1) \cdot$ jediný K-T vektor této úlohy. (Toto je analogie Věty O obálce $\tagDe{4.4.1}$)
Podle Věty $\tagDeHere{4.3.6}{./dualni-uloha}$ jsme popsali K-T vektory úlohy $\knvxProg$ pomocí řešení duální úlohy $\tagEqHere{4.3.1}{./dualni-uloha}$. Část 3. této věty jim navíc dává ještě charaketeristiku subgradientu hodnoty úlohy parametrického programování $\tagEq{4.4.2}$.
V případě regulární úlohy konvexního programování dostáváme zkombinováním
těcthotěchto dvou výsledků $\subdif F(b) = - Y\str(b)$, kde $Y\str(b)$ je množina řešení duální úlohy (viz Věta $\tagDeHere{4.3.6}{./dualni-uloha}$).
Pomocí Věty $\tagDe{4.4.3}$ jsme schopni dostat zajímavé výsledky o původní úloze matematického programování, tj. $\tagEq{4.4.2}$ s $b = 0$.
Důsledek $\D{4.4.4}$
Nechť množina $P \subseteq \R^n$ je konvexní, funkce $f, g_1, \dots, g_m$ jsou konvexní na $P$, platí $F(0) > - \infty$ a existuje $\bar x \in P$ takové, že $G(\bar x) < 0$ (viz Slaterova podmínka ve Větě $\tagDeHere{4.3.2}{./dualni-uloha}$). Potom $0 \in B$ a
- funkce $F(\cdot)$ je spojitá v bodě $b = 0$
- pro libovolné $h \in \R^m$ existuje jednostranná směrová derivace
$$F'_ h(0) = \max_ {y\str \in Y(0)} \scal {-y\str} h$$ - funkce $F$ je diferencovatelná v bodě $b = 0$ právě tehdy, když $Y(0)$ je jednoprvková množina, tj. $Y(0) = \brackets{y\str}$. Navíc platí $\gradT F(0) = -y\str$.
Z části 3. okamžitě plyne, že pokud existuje více K-T vektorů $\iff$ funkce $F$ není diferencovatelná
Fenchelova transformace a duální úloha
Lze ukázat, že pro $F(b)$ hodnotu primární úlohy je $F\str(y) = -\vf(y)$ a tedy duální úlohu $\tagEqHere{4.3.1}{./dualni-uloha}$ je možné psát jako $$ -F\str(y) \to \max, \quad y \geq 0 $$