Analýza citlivosti

$$ \xdef\scal#1#2{\langle #1, #2 \rangle} \xdef\norm#1{\left\lVert #1 \right\rVert} \xdef\dist{\rho} \xdef\and{\&}\xdef\brackets#1{\left\{ #1 \right\}} \xdef\parc#1#2{\frac {\partial #1}{\partial #2}} \xdef\mtr#1{\begin{pmatrix}#1\end{pmatrix}} \xdef\bm#1{\boldsymbol{#1}} \xdef\mcal#1{\mathcal{#1}} \xdef\vv#1{\mathbf{#1}}\xdef\vvp#1{\pmb{#1}} \xdef\ve{\varepsilon} \xdef\l{\lambda} \xdef\th{\vartheta} \xdef\a{\alpha} \xdef\vf{\varphi} \xdef\Tagged#1{(\text{#1})} \xdef\tagged*#1{\text{#1}} \xdef\tagEqHere#1#2{\href{#2\#eq-#1}{(\text{#1})}} \xdef\tagDeHere#1#2{\href{#2\#de-#1}{\text{#1}}} \xdef\tagEq#1{\href{\#eq-#1}{(\text{#1})}} \xdef\tagDe#1{\href{\#de-#1}{\text{#1}}} \xdef\T#1{\htmlId{eq-#1}{#1}} \xdef\D#1{\htmlId{de-#1}{\vv{#1}}} \xdef\conv#1{\mathrm{conv}\, #1} \xdef\cone#1{\mathrm{cone}\, #1} \xdef\aff#1{\mathrm{aff}\, #1} \xdef\lin#1{\mathrm{Lin}\, #1} \xdef\span#1{\mathrm{span}\, #1} \xdef\O{\mathcal O} \xdef\ri#1{\mathrm{ri}\, #1} \xdef\rd#1{\mathrm{r}\partial\, #1} \xdef\interior#1{\mathrm{int}\, #1} \xdef\proj{\Pi} \xdef\epi#1{\mathrm{epi}\, #1} \xdef\grad#1{\mathrm{grad}\, #1} \xdef\gradT#1{\mathrm{grad}^T #1} \xdef\gradx#1{\mathrm{grad}_x #1} \xdef\hess#1{\nabla^2\, #1} \xdef\hessx#1{\nabla^2_x #1} \xdef\jacobx#1{D_x #1} \xdef\jacob#1{D #1} \xdef\subdif#1{\partial #1} \xdef\co#1{\mathrm{co}\, #1} \xdef\iter#1{^{[#1]}} \xdef\str{^*} \xdef\spv{\mcal V} \xdef\civ{\mcal U} \xdef\knvxProg{\tagEqHere{4.1}{./nutne-a-postacujici-podminky-optimality} \, \and \, \tagEqHere{4.2}{nutne-a-postacujici-podminky-optimality}} $$

Nyní se budeme věnovat řešení úlohy matematické programování v závislosti na parametru.

První se podíváme na úlohu matematické programování s omezeními pouze ve tvaru rovností, ale s obecnou závislostí na parametrech.

A v druhém (a posledním) případě se podíváme na úlohu s omezeními ve tvaru nerovností, ale s parametry pouze v podobě absolutních členů ve funkcích zadávajících tyto omezení.

Zde je dobré podotknout, že druhý případ je mírně užitečnější a navíc si uvědomme, že 1 rovnost lze napsat jako 2 nerovnosti

Úlohy s rovnostmi

Věta $\D{4.4.1}$ (O obálce)

Mějme úlohu $$ f(x,r) \to \min, \qquad g_1(x, r) = 0, \; \dots, \; g_m(x,r) = 0 \tag{\T{AC.1}} $$ kde $x \in \R^n, r \in \R^k, f, g_1, \dots, g_m \in C^1$. Připusťme, že pro každou hodnotu parametru $r$ má úloha $\tagEq{AC.1}$ jediné řešení, které označíme $x\str (r)$. Potom hodnota úlohy $\tagEq{AC.1}$ je $$ f\str(r) = f(x\str(r), r). $$ Je-li $x\str(r)$ diferencovatelná vzhledem k $r$ a Jacobiho matice $\jacobx G(x\str (r), r) \in \R^{m\times n}$ má plnou hodnost $m$, pak platí $$ \parc {} {r_i}f\str(r) = \parc f {r_i} (x\str(r), r) + \sum_{j = 1}^m y_j\str(r) \parc {g_j} {r_i} (x\str(r), r) $$

Obálka je křivka, která se množiny křivek dotýká (tj. se dotýká každé křívky) a má společnou tečnu s danou křivkou

Jinak řečeno je tečná k množině křivek

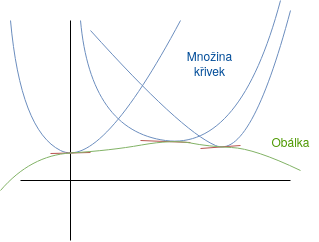
Požadavky Věty $\tagDe{4.4.1}$ jsou relativně silné, proto uveďme její "slabší verzi".

Věta $\D{4.4.2}$

Nechť $f, g_1, \dots, g_m \in C^2$ a $x\str$ je lokálním řešením úlohy $$ f(x) \to \min, \qquad g_1(x) = 0, \dots, g_m(x) = 0 $$ s odpovídajícími Lagrangeovými multiplikátory $y\str$. Nechť dále tato dvojice splňuje postačující podmínku druhého řádu, tj. $\hessx L(x\str, y\str) > 0$ na $\ker \jacob G(x\str)$, přičemž současně $x\str$ je regulárním bodem, tj. $\jacobx G(x\str) \in \R^{m\times n}$ má plnou hodnost $m$. Uvažme úlohu parametrického programování $$ f(x) \to \min, \qquad G(x) = u \tag{\T{AC.2}}, $$ pro parametr $u \in \R^m$. Pak existuje otevřená koule $S$ se středem v počátku ($u = 0$) taková, že pro každé $u \in S$ existuje lokální řešení $x\str(u) \in \R^n$ úlohy $\tagEq{AC.2}$ a odpovídající $y\str(u) \in \R^m$. Navíc $x\str(\cdot)$ a $y\str(\cdot)$ jsou spojitě diferencovatelné funkce na $S$ a platí $x\str(0) = x\str, y\str(0) = y\str$ a pro každé $u \in S$ máme $$ \grad f\str(u) = - y\str(u), $$ kde $f\str(u)$ značí optimální hodnotu úlohy $\tagEq{AC.2}$ vzhledem k $u$, tj. klademe $f\str(u) := f(x\str(u))$.

Jednoduše řečeno se optimální hodnota mění podle Lagrangeových multiplikátorů pro danou hodnotu $u$

Úlohy s nerovnostmi

Uvažujme úlohu závislou na $m$-tici