2. cvičení
$$ \xdef\mcal#1{\mathcal{#1}} \xdef\scal#1#2{\langle #1, #2 \rangle} \xdef\N{\mathbb N} \xdef\R{\mathbb R} \xdef\Q{\mathbb{Q}} \xdef\Z{\mathbb{Z}} \xdef\D{\mathbb{D}} \xdef\bm#1{\boldsymbol{#1}} \xdef\vv#1{\mathbf{#1}} \xdef\vvp#1{\pmb{#1}} \xdef\floor#1{\lfloor #1 \rfloor} \xdef\ceil#1{\lceil #1 \rceil} \xdef\grad#1{\mathrm{grad} , #1} \xdef\ve{\varepsilon} $$
Lineární model
Obecně má tvar $$ Y_i = \beta_0 + \beta_1 x_{i, 1} + \dots + \beta_k x_{i, k} + \ve_i, $$ kde $i = 1, \dots, n$. $Y_i$ je naše "cílová proměnná" (regresand). Proměnné $x_{i,1}, \dots, x_{i,k}$ jsou kovariáty (regresor, prediktor) a jsou pevně dané. Dále máme regresní koeficienty $\beta_0, \dots, \beta_k$ a $\varepsilon_i$ je náhodná proměnná chyby.
Také platí $$ \varepsilon_i \sim^{iid} (0, \sigma^2) $$ $$ E(\varepsilon_i) = 0 $$ $$ var(\varepsilon_i) = \sigma^2 $$ $$ cov(\varepsilon_i) = 0 $$
Celkem máme $$ \begin{pmatrix} Y_1 \ Y_2 \ \vdots \ Y_n \end{pmatrix} = \begin{pmatrix} 1 & x_{1,1} & \dots & x_{1, k} \ 1 & x_{2,1} & \dots & x_{2, k} \ \vdots & \vdots & \ddots & \vdots\ 1 & x_{n,1} & \dots & x_{n, k} \ \end{pmatrix} \cdot \begin{pmatrix} \beta_0 \ \beta_1 \ \vdots \ \beta_k \end{pmatrix} + \begin{pmatrix} \varepsilon_1 \ \varepsilon_2 \ \vdots \ \varepsilon_n \end{pmatrix} \tag{LSM} $$ A vektorově $$ \vv{Y} = \underbrace{\vv{X}}_{\text{matice plánu}} \cdot \vvp{\beta} + \vvp{\varepsilon} $$
Tedy pro 2. cvičení
02 / a)
$$FEV_i = \beta_0 + \ve_i$$
Můžeme si představit jako funkci $y = \beta_0$
A matice plánu bude
$$
\begin{pmatrix}
1 \
1 \
\vdots \
1
\end{pmatrix}
$$
Tedy kapacita plic je podle tohoto modelu konstantní a vizuálně znázorněné jako
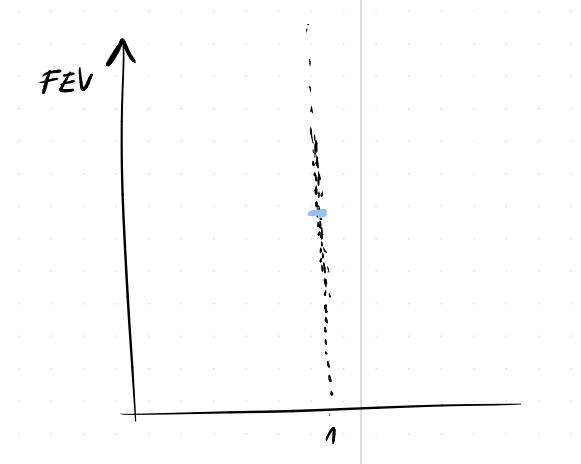
02 / c)
$$ FEV_i = \beta_0 + \beta_1 \cdot \text{Height}_i + \ve_i $$
Kapacitu plic modelujeme pomocí výšky. Tedy v tomto případě chceme funkci $y = \beta_0 + \beta_1 x$.
A graficky
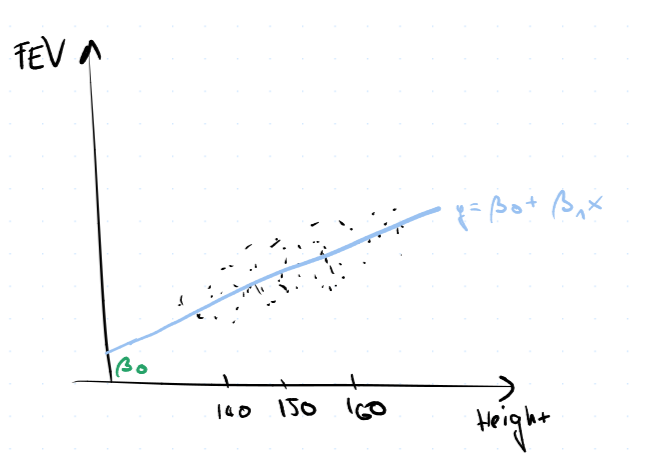A matice plánu tentokrát bude
$$
\begin{pmatrix}
1 & \text{Height}_1 \
1 & \text{Height}_2 \
\vdots \
1 & \text{Height}_n
\end{pmatrix},
$$
což dosazujeme do $(LSM)$.
Tedy máme model hledáme $y = \beta_0 + \beta_1 x$ a zde
- $\beta_0$ ... střední hodnota predikce při nulových hodnotách ostatních prediktorů
- $\beta_1$ ... nárůst střední hodnoty predikce při nárůstu výšky (prediktor $\text{Height}$) o 1 cm
02 / b)
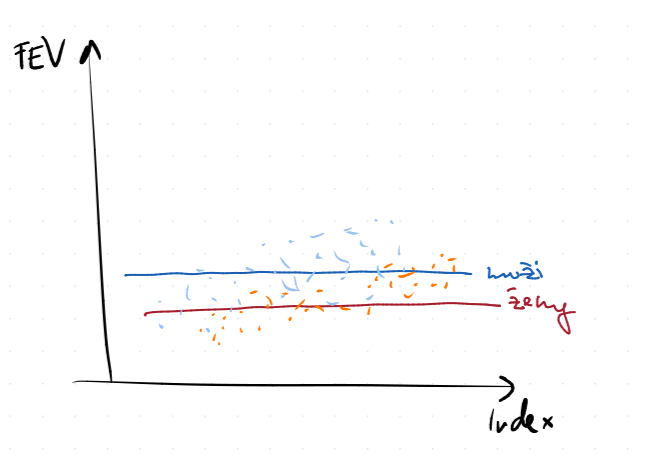
$$ FEV_i = \beta_0 + \beta_1 \cdot \text{Sex}_i + \ve_i $$
a $\beta_1$ zde reprezentuje rozdíl predikce mezi muži a ženami s maticí plánu $$ \begin{pmatrix} 1 & 1 \ 1 & 0 \ \vdots \ 1 & 1 \end{pmatrix}, $$
kde $1$ reprezentuje muže.
A graficky
02/ d)
$$ FEV_i = \beta_0 + \beta_1 \cdot \text{Height}_i + \beta_2 \text{Height}_i^2 + \ve_i $$ V tomto případě je $\beta_1, \beta_2$ jsou složité na interpretaci
A matice plánu by v tomto případě byla $$ \begin{pmatrix} 1 & \text{Height}_1 & \text{Height}^2_1 \ 1 & \text{Height}_2 & \text{Height}^2_2 \ \vdots \ 1 & \text{Height}_n & \text{Height}^2_n \end{pmatrix}, $$
02 / e)
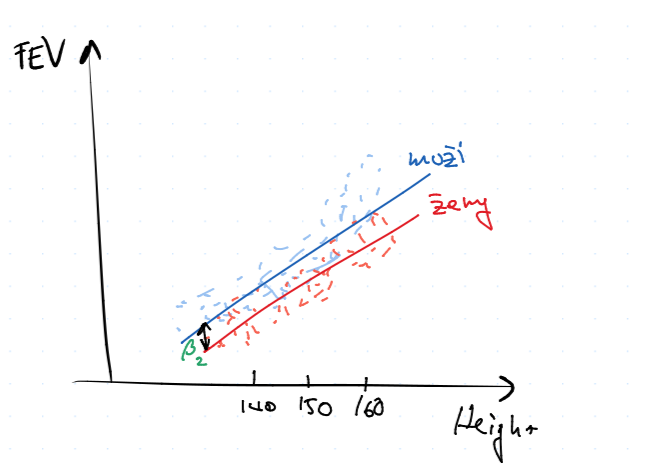
$$ FEV_i = \beta_0 + \beta_1 \cdot \text{Height}_i + \beta_2 \text{Sex}_i + \ve_i $$ s maticí plánu $$ \begin{pmatrix} 1 & \text{Height}_1 & 0 \ 1 & \text{Height}_2 & 1 \ \vdots \ 1 & \text{Height}_n & 1 \end{pmatrix}, $$ přičemž ve 3. sloupci jsou $1$ značí muže.
A hledáme přímku $$ y = \beta_0 + \beta_1 x + \beta_2 \vv I {\text{Sex} = \text{"male"}} $$
s významem koeficientů
- $\beta_0$ ... střední hodnota predikce při nulových hodnotách ostatních prediktorů (nulová výška a ženské pohlaví)
- $\beta_1$ ... změna střední hodnoty predikce při nárůstu výšky (prediktor $\text{Height}$) o 1 cm pro ženy
- $\beta_2$ ... rozdíl střední hodnoty predikce mezi muži a ženami
02 / g)
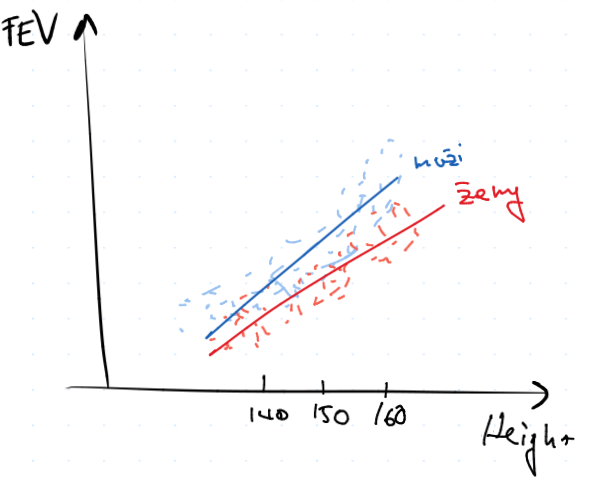
$$ FEV_i = \beta_0 + \beta_1 \cdot \text{Height}_i + \beta_2 \text{Sex}_i + \beta_3 (\text{Sex}_i \times \text{Height}_i) + \ve_i, $$ kde členu $\text{Sex}_i \times \text{Height}_i$ interakce a matice plánu bude $$ \begin{pmatrix} 1 & \text{Height}_1 & 0 & 0 \ 1 & \text{Height}_2 & 1 & \text{Height}_2 \ 1 & \text{Height}_3 & 0 & 0 \ \vdots & \vdots & \vdots & \vdots \ 1 & \text{Height}_n & 1 & \text{Height}_n \end{pmatrix}, $$ přičemž ve 3. sloupci jsou $1$ značí muže.
A hledáme přímku $$ y = \beta_0 + \beta_1 x + \beta_2 \vv I {\text{Sex} = \text{"male"}} + \beta_3 x \vv I {\text{Sex} = \text{"male"}}, $$ tj.
- žena ... $y = \beta_0 + \beta_1 x$
- muž ... $y = (\beta_0 + \beta_2) + (\beta_1 + \beta_3)x$
Zde $\beta_3$ značí rozdíl střední hodnoty predikce mezi muži a ženami při nárůstu výšky o 1 cm
rozdíl rychlosti růstu $\text{FEV}$ mezi muži a ženami
